网络流【待续】

2018-04-23

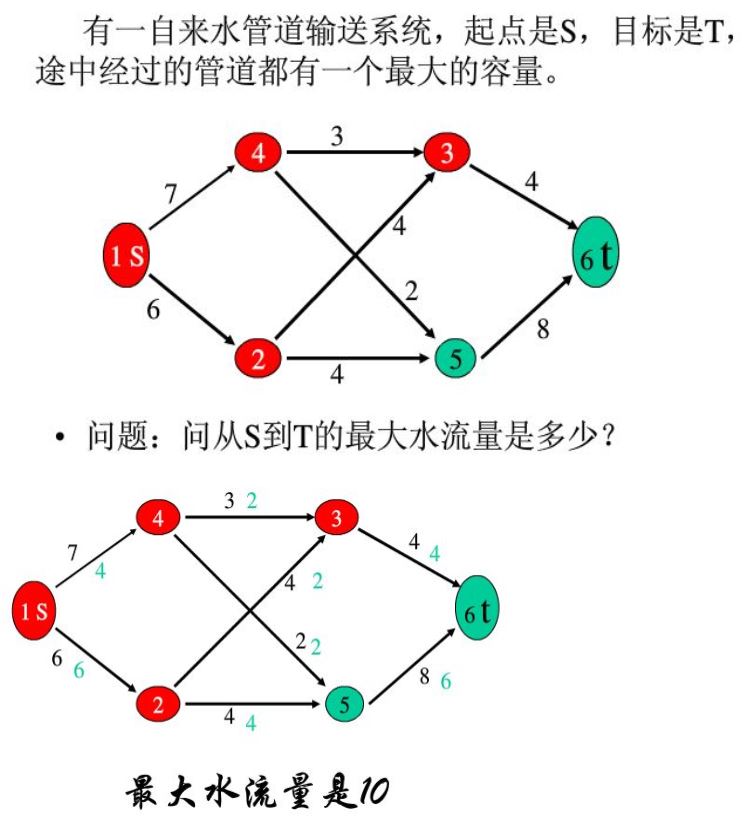
例如：有一个自来水管道输送系统，起点是S，目标是T，图中经过的管道都有一个最大的容量：

网络流的定义

在有向图G=（V,E）中：

1、有唯一的一个源点S（入度为0：出发点）

2、有唯一的一个汇点（出度为0：结束点）

3、图中的每条弧（u,v）都有一个非负的容量c（u,v）

满足上述条件的图G称为网络流图。

记为：G=（V,E,C）

可行流

每条管道中可以通过的流量。

最大流

在所有的可行流中，流量最大的一个流。（最大流可能不止一个）

解决最大流的问题常用到Ford-Fulkerson方法（在此方法下，存在着若干种不同时间复杂度下的实现）

Ford-Fulkerson和Edmonds-Karp

1、残存网络

第一个图是流网络，边上的12/16,12指的是流量，16是容量。

第二个图是残存网络，可能会存在一对相反的边，如刚刚12/16在残存网络中，体现为 v1->s = 12，s->v1 = 16-12。与流网络中对应的边代表的是该边的残余容量，流网络中不存在的边是一条反向的已有流量边，这部分流量可以通过回流减少。（残存网络中值为0的边不画出）

2、增广路径

假如有这么一条路，这条路从源点开始一直一段一段的连到了汇点，并且，这条路上的每一段都满足流量<容量，注意，是严格的<,而不是<=。那么，我们一定能找到这条路上的每一段的(容量-流量)的值当中的最小值delta。我们把这条路上每一段的流量都加上这个delta，一定可以保证这个流依然是可行流，这是显然的。这样我们就得到了一个更大的流，他的流量是之前的流量+delta，而这条路就叫做增广路。

3、方法

我们不断地从起点开始寻找增广路，每次都对其进行增广，直到源点和汇点不连通，也就是找不到增广路为止。当找不到增广路的时候，当前的流量就是最大流，这个结论非常重要。

寻找增广路的时候我们可以简单的从源点开始做bfs，并不断修改这条路上的delta量，直到找到源点或者找不到增广路。

4、代码

int c[MAX][MAX];  //残留网络容量
int pre[MAX];  //保存增广路径上的点的前驱顶点
bool visit[MAX];

int Ford_Fulkerson(int src,int des,int n){   //src：源点 des：汇点 n：顶点个数
     int i,_min,total=0;
     while(true){
         if(!Augmenting_Path(src,des,n))return total; //如果找不到增广路就返回，在具体实现时替换函数名
         _min=(1<<30);
         i=des;
         while(i!=src){   //通过pre数组查找增广路径上的边，求出残留容量的最小值
             if(_min>c[pre[i]][i])_min=c[pre[i]][i];
             i=pre[i];
         }
         i=des;
         while(i!=src){    //再次遍历，更新增广路径上边的流值
             c[pre[i]][i]-=_min;
             c[i][pre[i]]+=_min;
             i=pre[i];
         }
         total+=_min;     //每次加上更新的值
     }
}

int dfs(int u,int t,int f)
{
	if(u==t)
	  return f;
	  used[u]=1;
	for(int i=0;i<g[u].size();i++)
	{
		Edge &e=g[u][i];
		int v=e.to;
		if(!used[v]&&e.cap>0)
		{
			int d=dfs(v,t,min(e.cap,f));
			if(d>0)
			{
				e.cap-=d;
				g[e.to][e.rev].cap+=d;
				return d;
			}
		}
	}
	return 0;
}
int max_flow(int s,int t)
{
	int res=0,f;
	while(1)
	{
		f=INF;
		memset(used,0,sizeof(used));
		int d=dfs(s,t,f);
		if(d<=0)
			break;
		res+=d;
	}
	return res;
}

--*
    Ford-fulkerson最短扩充路
    调用前输入残余矩阵 g[][]
    直接调用max_flow(源点, 汇点) 返回最大流
    
    注意初始化：nodeNum（节点总数量）
    注意节点标号： 0 - (nodeNum-1)
*/
//pku1273
#include <stdio.h>
#include <string.h>

const int MAXN = 201;

int g[MAXN][MAXN];        //残留网络，初始为原图
int flow[MAXN][MAXN];
int nodeNum;            //节点总数量
int pre[MAXN];

//bfs找增广路
int bfs(const int &s, const int &t)
{
    int que[201], p, q, v, i;
    for (i = 0; i < nodeNum; i++)
        pre[i] = -1;  
    que[0] = s;
    pre[s] = s;
    p = 0, q = 1;
    while (p < q)
    {
        v = que[p++];
        for (i = 0; i < nodeNum; i++)
            if (pre[i] == -1 && (flow[v][i] < g[v][i] || flow[i][v] > 0))
            {
                pre[i] = v;
                que[q++] = i;
                if (i == t) return 1;
            }
    }
    return 0;
}

//修改残留矩阵和增广路
void track_back(const int &s, const int &t)
{
    int i = t, v, min = 0x7fffffff;
    while (i != s)
    {
        v = pre[i];
        if (flow[v][i] < g[v][i])
        {
            if(min > g[v][i] - flow[v][i])
                min = g[v][i] - flow[v][i];
        }
        else
            if (flow[i][v] > 0)
            {
                if(min > flow[i][v])
                    min = flow[i][v];
            }
        i = v;
    }
    i = t;
    while (i != s)
    {
        v = pre[i];
        if (flow[v][i] < g[v][i])
            flow[v][i] += min;
        else
            if (flow[i][v] > 0)
                flow[i][v] -= min;
        i = v;
    }
}

//返回 从节点s到节点t的最大流
int max_flow(const int &s, const int &t)
{
    while (bfs(s, t))
        track_back(s, t);
    int res = 0, i;
    for (i = 0; i < nodeNum; i++)
        if (i != s) res += flow[s][i];
    return res;
}

int main()
{
    int m, b, e, c;
    while(scanf("%d%d", &m, &nodeNum)!=EOF)
    {
        memset(g, 0, sizeof(g));
        memset(flow, 0, sizeof(flow));
        while (m--)  
            scanf("%d %d %d", &b, &e, &c), g[b - 1][e - 1] += c;
        printf("%d\n", max_flow(0, nodeNum-1));
    }
    return 0;
}

最小割

就是从图G(V,E)中去除一些边，使得图G中源点S到终点T不连通。如果去除的这些边的权和最小，就是最小割。这个权和可以证明等于网络的最大流量！因此，最大流等价于最小割。求解最大流问题，也可以转化为最小割。求最大流和求最小割集是两类不同的算法。求解最小割集普遍采用Stoer-Wagner算法。

Stoer-Wagner

int min_cut(int now)
{
    int ret = INF;
    for(int i = 0; i < n; i++) node[i] = i;
    while(now > 1) {
        int k, pre = 0;
        memset(vis, 0, sizeof(vis));
        memset(dis, 0, sizeof(dis));
        for(int i = 1; i < now; i++) {
            k = -1;
            for(int j = 1; j < now; j++) if(!vis[node[j]]) {
                dis[node[j]] += G[node[pre]][node[j]];
                if(k == -1 || dis[node[k]] < dis[node[j]]) {
                    k = j;
                }
            }
            vis[node[k]] = true;
            if(i == now - 1) {
                ret = min(ret, dis[node[k]]);
                for(int j = 0; j < now; j++) {
                    G[node[pre]][node[j]] += G[node[j]][node[k]];
                    G[node[j]][node[pre]] = G[node[pre]][node[j]];
                }
                node[k] = node[--now];
            }
            pre = k;
        }
    }
    return ret;
}