2018暑期训练题解

2018-08-11

7.7 [BAPC 2014 Preliminary](https://www.jisuanke.com/contest/1403)

A. 思维题，重点在于当剩余的n<k时，只要k%n==0就可以成功，比如 64 6的时候，先约分：32：6，再约：16:6，一直约到 1:6 ，那n=1，当然ok。

B. dijkstra最短路一下

D. Dp，结束后想了一下，dp[i]表示第i层停下来的所有怨气，dp[i]=min(dp[i],dp[j] + val(j->i)) ,（j<i）i之前电梯停在j层，然后从j直接到i 的话，加上这一部分的怨气就好了val，而valij的怨气就是i的前缀和加上若每一层都停的怨气，再减去了j层停下来的人消失的这部分怨气。

F. 飞行航道水

J. 找单词，八方找，正反找。看了题解好像是先判断了一下回文减少了一下长度？

7.10 [ Benelux Algorithm Programming Contes](https://www.jisuanke.com/contest/1404)

B. 最少按下的按钮次数

用bfs，时间小于0，变成0，大于3600，变为3600。vis[i]记录时间为i的最少步骤数目。

#include <bits/stdc++.h>
using namespace std;
const int N=110;
int n,sum;
int a[20],vis[3610];
struct node{
    int val;
    int step;
};
void solve()
{
    queue<node>q;
    node temp,tp;
    temp.val=0;
    temp.step=0;
    q.push(temp);
    vis[0]=0;
    while(!q.empty())
    {
        temp=q.front();
        q.pop();
        for(int i=0;i<n;i++)
        {
            int cur=temp.val+a[i];
            if(cur<0) cur=0;
            else if(cur>3600) cur=3600;
            if(vis[cur]==-1)
            {
                vis[cur]=temp.step+1;
                tp.step=temp.step+1;
                tp.val=cur;
                q.push(tp);
            }
        }
    }
}
int main()
{
    int t;

    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&sum);
        for(int i=0;i<n;i++)
            scanf("%d",&a[i]);
        memset(vis,-1,sizeof(vis));
        solve();
        for(int i=sum;i<=3600;i++)
            if(vis[i]!=-1)
        {
            printf("%d %d\n",vis[i],i-sum);
            break;
        }
    }
    return 0;
}

G. 水

I. 计算组成n的最小的两个斐波那契数a b，其中按b小来排，且a<b

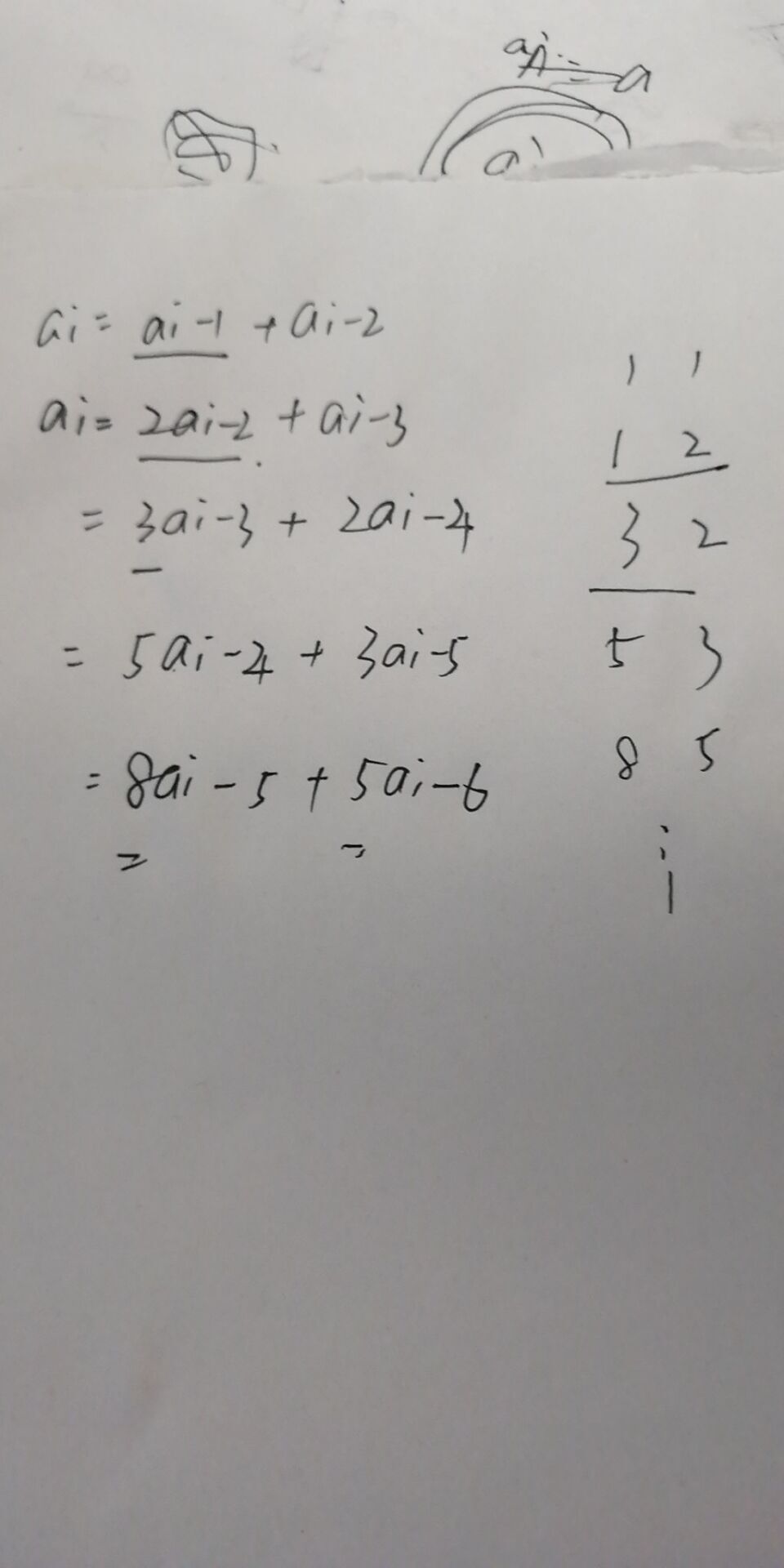
由上可知，先计算出最大的两个相邻数相加小于n的地方，设为x，y（x<y），然后xa+yb=n,从b=1开始求满足条件的a，且a<b。

#include <bits/stdc++.h>
using namespace std;
int a[1000];
const int INF=0x3f3f3f3f;
int main()
{
    a[0]=a[1]=1;
    for(int i=2;i<44;i++)
        a[i]=a[i-1]+a[i-2];
    //小于1e9的斐波那契
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n;
        scanf("%d",&n);
        int loc;
        //计算出最大的两个相邻数相加小于n的地方
        for(int i=43;i>=1;i--)
        {
            if((a[i]+a[i-1])<=n)
            {
                loc=i;break;
            }
        }
        int ai_1;
        while(loc>0)
        {
            for(int i=1;i*a[loc]<n;i++)
            {
                if((n-a[loc]*i)%a[loc-1]==0&&(n-a[loc]*i)/a[loc-1]<=i)
                {
                    ai_1=i;goto out;
                }
            }
            loc--;
        }
    out:
        printf("%d %d\n",(n-a[loc]*ai_1)/a[loc-1],ai_1);
    }
    return 0;
}

J. 把迷宫设置大，然后从中间模拟

7.12

B. 最小路径覆盖，网络流，最大流

#include <bits/stdc++.h>
using namespace std;
const int N=5010;
const int M=3000010;
const int inf=0x3f3f3f3f;
struct Edge
{
    int v,cap,nxt;
}e[M];;//邻接表要开边数的两倍
int src,des,dis[N],head[N],ecnt;  //memset dis,head-1 ecnt=0,src=0,des=2*n+1;
int n,m;
void Addedge(int u,int v,int w)
{
    e[ecnt].v=v;
    e[ecnt].cap=w;
    e[ecnt].nxt=head[u];
    head[u]=ecnt++;
    e[ecnt].v=u;
    e[ecnt].cap=0;
    e[ecnt].nxt=head[v];
    head[v]=ecnt++;
}
bool Bfs()
{
    queue<int>q;
    q.push(src);
    memset(dis,-1,sizeof(dis));
    dis[src]=0;
    while(!q.empty())
    {
        int u=q.front();q.pop();
        for(int i=head[u];~i;i=e[i].nxt)
        {
            int v=e[i].v;
            if(e[i].cap>0&&dis[v]==-1)
            {
                dis[v]=dis[u]+1;
                q.push(v);
            }
        }
    }
    return dis[des]>=0;
}
int Dfs(int u,int a)
{
    if(u==des) return a;
    for(int i=head[u];~i;i=e[i].nxt)
    {
        int v=e[i].v,t=0;
        if(e[i].cap>0&&dis[v]==dis[u]+1&&(t=Dfs(v,min(a,e[i].cap))))
        {
            e[i].cap-=t;
            e[i^1].cap+=t;
            return t;
        }
    }
    dis[u]=-1;
    return 0;
}
int Dinic()
{
    int ans=0;
    while(Bfs())
    {
        int t=0;
        while(t=Dfs(src,inf)) ans+=t;
    }
    return ans;
}
int main()
{
    int num,u,v;
    ecnt=0;
    memset(head,-1,sizeof(head));
    scanf("%d",&num);
    src=0;des=2*num+1;
    for(int i=1;i<=num;i++)
        Addedge(0,i,1);
    for(int i=num+1;i<=2*num;i++)
        Addedge(i,2*num+1,1);
    for(int i=1;i<=num;i++)
    {
        scanf("%d",&u);
        while(u--)
        {
            scanf("%d",&v);
            Addedge(i,num+v+1,1);
        }
    }
    n=num+2;
    printf("%d\n",num-Dinic());
    return 0;
}

E. 求次短路是否等于最短路长。

#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
#define MAXN (10000 + 10)
#define INF (5000*5000*2)
using namespace std;

struct edge
{
    int to, cost;
    edge(int tv = 0, int tc = 0):
        to(tv), cost(tc) {}
};
typedef pair<int,int> P;
int N, R;
vector<edge> graph[MAXN];
int dist[MAXN];     //最短距离
int dist2[MAXN];    //次短距离

void solve()
{
    fill(dist, dist+N, INF);
    fill(dist2, dist2+N, INF);
    //从小到大的优先队列
    //使用pair而不用edge结构体
    //是因为这样我们不需要重载运算符
    //pair是以first为主关键字进行排序
    priority_queue<P, vector<P>, greater<P> > Q;
    //初始化源点信息
    dist[0] = 0;
    Q.push(P(0, 0));
    //同时求解最短路和次短路
    while(!Q.empty())
    {
        P p = Q.top();
        Q.pop();
        //first为s->to的距离，second为edge结构体的to
        int v = p.second, d = p.first;
        //当取出的值不是当前最短距离或次短距离，就舍弃他
        if(dist2[v] < d) continue;
        for(unsigned i = 0; i < graph[v].size(); i++)
        {
            edge &e = graph[v][i];
            int d2 = d + e.cost;
            if(dist[e.to] > d2)
            {
                swap(dist[e.to], d2);
                Q.push(P(dist[e.to], e.to));
            }
            if(dist2[e.to] > d2 && dist[v] < d2)
            {
                dist2[e.to] = d2;
                Q.push(P(dist2[e.to], e.to));
            }
        }
    }
}
int main()
{
    int A, B, D,K;
    scanf("%d%d%d", &N, &R,&K);
    while(K--)
        scanf("%d",&A);
    for(int i = 0; i < R; i++)
    {
        scanf("%d%d%d", &A, &B, &D);
        graph[A-1].push_back(edge(B-1, D));
        graph[B-1].push_back(edge(A-1, D));
    }
    solve();
    if(dist2[N-1]==dist[N-1])
        printf("yes\n");
    else
        printf("no\n");
    return 0;
}

F. 求大数因子个数，用大数分解求出质因数

7-12German Collegiate Programming Contes…

7-14 https://www.jisuanke.com/contest/1444

7-17The 2018 ACM-ICPC Chinese Collegiate…

7-19 German Collegiate Programming Contes…

7.23 [多校1 ](http://acm.hdu.edu.cn/contests/contest_show.php?cid=802)

1001 Maximum Multiple 水。

1002 Balanced Sequence 贪心题。对于左右括号的情况分类，然后按照规则排序。具体见代码。

#include <bits/stdc++.h>
#pragma comment(linker, “/STACK:1024000000,1024000000”)
using namespace std;
struct node{
    int left_no,right_no,yes;
    node()
    {
        left_no=right_no=yes=0;
    }
};
bool cmp(node a,node b)
{
    if(a.left_no>=a.right_no&&b.left_no<=b.right_no)//左少右多 + 左多右少 a前面
        return true;
    if(a.left_no<=a.right_no&&b.left_no>=b.right_no) //左少右多 + 左多右少 b前面
        return false;
    if(a.left_no<=a.right_no&&b.left_no<=b.right_no) //左少右多+左少右多 谁的左面数量多谁放前面
        return a.left_no>b.left_no;
    return a.right_no<b.right_no; // 左多右少 左多右少 谁的右边多谁放后面

}
char s[5000010];
int main()
{
    int n,t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        vector<node>a(n);
        int len;
        for(int i=0;i<n;i++)
        {
            scanf("%s",s);
            len=strlen(s);
            long long left=0,right=0,ans=0;
            for(int j=0;j<len;j++)
            {
                if(s[j]=='(')
                    left++;
                else
                {
                    if(left>0)  left--,ans++;
                    else    right++;
                }
            }
            a[i].left_no=left;
            a[i].right_no=right;
            a[i].yes=ans;
        }
        sort(a.begin(),a.end(),cmp);
        long long left=0,right=0,ans=0;
        for(int i=0;i<n;i++)
        {
            ans+=a[i].yes;
            if(left>=a[i].right_no)
                left-=a[i].right_no,ans+=a[i].right_no;
            else
                ans+=left,left=0;
            left+=a[i].left_no;
        }
        printf("%lld\n",ans*2);
    }
    return 0;
}

1003 Triangle Partition 水。对x,y按照升序排序再每次取三个就好了。

1004 Distinct Values 给你一个n，一个q，表示数列中有n个元素，q个区间询问，每次一个[l,r]，表示此区间内的数字不能有重复，要求输出最小字典序的。用set维护一下区间内的数字出现情况就好了。

#include <bits/stdc++.h>
using namespace std;
bool cmp(pair<int,int>a,pair<int,int>b)
{
    if(a.first==b.first)
        return a.second>b.second;
    return a.first<b.first;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n,q,l,r;
        scanf("%d%d",&n,&q);
        set<int>val;
        vector<pair<int,int> >p;
        vector<int>x(n+5);
        for(int i = 1 ;i <= n ; i++)
            p.push_back( make_pair(i,i) );
        for(int i=1;i<=n;i++)
            val.insert(i);
        for(int i=1;i<=n;i++)
            x[i]=1;
        for(int i=0;i<q;i++)
        {
            scanf("%d%d",&l,&r);
            p.push_back(make_pair(l,r));
        }
        sort(p.begin(),p.end());
        int left=1,cur=1;
        set<int>::iterator it,bef;
        for(int i=0;i<p.size();i++)
        {
            while(left<p[i].first)
                val.insert(x[left++]);
            for(it=val.begin();it!=val.end()&&cur<=p[i].second;)
            {
                x[cur++]=*it;
                int s=*it;
                it++;
                val.erase(s);
            }
        }
        for(int i=1;i<=n-1;i++)
            printf("%d ",x[i]);
        printf("%d\n",x[n]);
    }
    return 0;
}

1007 Chiaki Sequence Revisited 数学题。

#include <bits/stdc++.h>
#define mst(a,b) memset(a,b,sizeof(a))
#define ALL(x) x.begin(),x.end()
#define pii pair<int,int>
#define eps 1e-4
inline long long lowbit(long long x){return x&-x;}
const int N = 1e6+10;
const long long mod = (long long)1e9+7;
const int INF=0x3f3f3f3f;
const long long LINF=(1LL<<62);
typedef long long LL;
typedef unsigned long long ULL;
//#define LOCAL
const double PI = acos(-1.0);
using namespace std;

LL n,inv2,p[63];

LL q_pow(LL base, LL b){
  LL res = 1;
  while(b){
    if(b&1) res = res*base%mod;
    base = base*base%mod;
    b>>=1;
  }
  return res;
}
bool check(LL x){   //为什么要这么写呢，看上面打的表，除以每个2^i就可以得出2^i有多少个，这样子加完就得到对应的a[x]是多少。
  LL temp = 0;
  for(int i = 0; i <= 62; i++){
    temp += x/p[i];
    if(temp >= n-1) return true;
  }
  return temp >= n-1;
}
LL cal(LL x){
  LL temp = 0;
  for(int i = 0; i <= 62; i++) temp += x/p[i];
  return temp;
}
int main(){
#ifdef LOCAL
    freopen("out.txt", "w", stdout);
#endif // LOCAL
    inv2 = q_pow(2,mod-2);  //2的逆元，等下等差数列求和的时候要用
    p[0] = 1;
    for(int i = 1; i <= 62; i++) p[i] = p[i-1]*2; //预处理2^i
    int T; scanf("%d",&T);
    while(T--){
      scanf("%lld",&n);
      if(n==1){
        printf("1\n");
        continue;
      }
      LL l = max(1LL,n/2-30), r = min(n,n/2+30), mid, pos;
      while(l<=r){
        mid = (l+r)>>1;
        if(check(mid)){   //二分找n对应的a[n]；
          pos = mid;      //pos即为a[n]
          r = mid-1;
        }else l = mid+1;
      }
      LL res = pos-1, now = 0;  //这里pos-1是因为在a[n]位置的n可能不是刚好符合2^i，所以要找前面一个，前面一个必定是符合2^i个的。
      for(int i = 0; i <= 62; i++){
        if(p[i]>res) break;
        LL temp = res/p[i];
        temp %= mod;
        now = (now+p[i]%mod*(temp+1)%mod*temp%mod*inv2%mod)%mod;  //等差数列求和，不要忘记Mod
      }
      now = (now+(n-1-cal(res)%mod)%mod*pos%mod)%mod;  //剩下这里就是那些不完整的a[n]了
      printf("%lld\n",(1+now)%mod);
    }
    return 0;
}

1011 Time Zone 水。

7.25 [ 多校2](http://acm.hdu.edu.cn/contests/contest_show.php?cid=803)

1003 Cover 没看题，听了题解，大概是给你一个无向图，让你求至少要多少一笔画才能把它画完。一笔画有两种情况，一种是欧拉路，一种是欧拉回路，也就是说，对于图中的所有点，度数为奇数的要么是0（回路），要么是2（一个进来的点，一个出去的点）。所以要把一个图构造成欧拉路/回路的话，就意味着要在图中x个奇数度的点中连接x/2条边，然后在对于新生成的图，找欧拉路，然后再把添上去的x/2条边删去，分成的几条路就是一笔画的结果。

1004 Game 水题，先手必赢。先手可以取或者不取1。

1005 Hack It 不知所措的构造题。要求是构造出一个n*n(n<=2000)的矩阵，你可以在里面填黑点，但是你不能让任意四个黑点组成一个矩形（四个角），要求是至少包含85000个黑点。老实说，我无法理解构造方法。

1007 Naive Operations 线段树题解

1010 Swaps and Inversions 水题。数逆序数对，再乘以min(x,y)即可。这里我发现逆序数对数有x个，就可以通过交换相邻数字x次使得它不存在逆序数。

用归并排序可以得到逆序数对个数。

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm>
#define MOD 1000000007
using namespace std;
typedef long long ll;
long long sum;
int a[500005];
int temp[500005];
void sort2(int a[],int l,int mid,int r)
{
    int i=l,j=mid+1,k=0;
    while(i<=mid&&j<=r)
    {
        if(a[i]<=a[j])
        {
            temp[k++]=a[i++];
        }
        else
        {
            temp[k++]=a[j++];
            sum+=mid-i+1;
        }
    }
    while(i<=mid)  temp[k++]=a[i++];
    while(j<=r)    temp[k++]=a[j++];

    for(int i=l,k=0; i<=r; k++,i++)
        a[i]=temp[k];
}

void sort1(int a[],int l,int r)
{
    int mid;
    if(l<r)
    {
        mid=(l+r)/2;
        sort1(a,l,mid);
        sort1(a,mid+1,r);
        sort2(a,l,mid,r);
    }
}
int main()
{
    int n;
    long long x,y;
    while(scanf("%d%lld%lld",&n,&x,&y)!=EOF)
    {
        sum=0;
        for(int i=0; i<n; i++)
            scanf("%d",&a[i]);
        sort1(a,0,n-1);
        printf("%lld\n",sum*min(x,y));
    }
    return 0;
}

7.24 [ The 2018 ACM-ICPC China JiangSu Prov..](https://www.jisuanke.com/contest/1408)

A. Plague Inc 水题暴力，遍历每个点到感染源的路求最远。

B. Array n个数，k对逆序数，求可能的方案数。这是一道DP 。

D. Persona5 公式题

E. Massage 公式结论题

I. T-shirt ////////////////////////////////////

J. Set 结论是(n+1)!-1，用java写

K. Road 连通图，删去尽可能多的路，使得每个城市到第0号城市的最短路长度不变，求可能的方案数量。

用floyd先求出每个城市之间的最短路，然后对每条0~~i城市的最短路，判断0~~j城市的距离加上i到j的原始距离是否还和最短路相等，相等的话，在j城市上的最短路径+1。最后将他们乘起来。

#include <bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=350;
const long long MOD=1e9+7;
int dist[maxn],g[maxn][maxn],f[maxn][maxn],N;
long long road[maxn];
long long floyd()
{
    long long ans=1;
    memset(road,0,sizeof(road));

    for (int k=0;k<N;k++)
        for (int i=0;i<N;i++)
            for (int j=0;j<N;j++)
                if (i!=k&&i!=j&&j!=k)
                    g[i][j]=min(g[i][j],g[i][k]+g[k][j]);
    g[0][0]=0;
    for(int i=0;i<N;i++)
        for(int j=0;j<N;j++)
        if(i!=j&&g[0][i]+f[i][j]==g[0][j])
    {
        road[j]++;
    }
    for(int i=1;i<N;i++)
        if(road[i])
            ans=(ans*road[i])%MOD;
    return ans;

int main()
{
    while(scanf("%d",&N)!=EOF)
    {
        memset(g,INF,sizeof(g));
        string s;
        for(int i=0;i<N;i++)
        {
            cin>>s;
            for(int j=0;j<s.size();j++)
            {
                if(s[j]=='0')
                    f[i][j]=g[i][j]=INF;
                else
                	f[i][j]=g[i][j]=s[j]-'0';
            }
        }
        printf("%lld\n",floyd());
    }
    return 0;
}

7.26 [ Nordic Collegiate Programming Contes...](https://www.jisuanke.com/contest/1410)

A. Adjoin the Networks 回头补把。

B. Bell Ringing 用生成全排列的邻位互换法：（具体方法解释可以看排列组合的文章）

仔细想想不就是把n插入到已完成的n-1阶排列的不同位置中得到n阶排列吗？

n=1; 1

n=2; 12 , 21

n=3; 123, 132, 312, 321, 231, 213

……

用这种方法可以产生出任意n阶全排列，（而且符合bellring中的移动规律，即每个数移动的位置最多为1，就能一下子构造出n！个不重复的全排列）

#include <bits/stdc++.h>
using namespace std;
int n;
int A[15];
int dir[15];

void print()
{
    for(int i=1;i<n;i++)
        printf("%d ",A[i]);
    printf("%d\n",A[n]);
}
bool IF_Active(int i) //判断是否活跃（前面的数字比它小就是活跃）
{
    if(i+dir[i]<=0||i+dir[i]>n)
        return false;
    if(A[i+dir[i]]<A[i])
        return true;
    return false;
}

int MAX_Active() //找到最大的活跃数字
{
    int id=n+1;
    for(int i=1;i<=n;i++)
    {
        if(IF_Active(i)&&A[id]<A[i])
            id=i;
    }
    return id;
}
int Swap(int i) //交换最大的活跃数字和它前面的那个数字，注意方向也要交换
{
    int c=A[i];
    A[i]=A[i+dir[i]];
    A[i+dir[i]]=c;

    c=dir[i];
    dir[i]=dir[i+c];
    dir[i+c]=c;

    return i+c;
}
void UPdate(int index)
{
    for(int i=1;i<=n;i++)
    {
        if(A[index]<A[i])
            dir[i]=-dir[i];
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        A[i]=i;
        dir[i]=-1;
    }
    print();
    
    while(1)
    {
        int id=MAX_Active();
        if(id==n+1) break;
        id=Swap(id);
        UPdate(id);
        print();
    }
    return 0;
}

C. Cryptographer’s Conundrum 水

D. Disastrous Downtime 水，取最大的ai~ai+1000范围内的数字个数即可。

E.Entertainment Box n个节目，k个录像带，给出每个节目的播放时间，求最多能录几个节目。

用multiset维护当前正在录制的所有节目的结束时间，二分找到最接近下一个要录的节目的起始时间且小于起始时间的录像带，把这个录像带中的r替换成下一个要录的节目，cnt++，如果没有找到并且集合的size还不到k个的话，就直接把r放进去，cnt++。最后输出cnt。

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10;
struct node
{
    int l,r;
} nn[N];
bool cmp(node a,node b)
{
    if(a.r==b.r)
        return a.l<b.l;
    return a.r<b.r;
}

multiset<int>q;
multiset<int>::iterator pos;
int main()
{
    int n,k;
    int cnt=0;
    int i;
    scanf("%d%d",&n,&k);
    for(int i=0; i<n; i++)
        scanf("%d%d",&nn[i].l,&nn[i].r);
    sort(nn,nn+n,cmp);
    for(i=0; i<n; i++)
    {
        if(q.empty())
        {
            cnt++;q.insert(nn[i].r);
            continue;
        }
        if(*q.begin()>nn[i].l)
        {
            if(q.size()<k)
            {
                cnt++;q.insert(nn[i].r);
            }
            continue;
        }
        pos=q.upper_bound(nn[i].l);
        pos--;
        if(*pos<=nn[i].l)
        {
            cnt++;
            q.erase(pos);
            q.insert(nn[i].r);
        }
        else
        {
            if(q.size()<k)
            {
                cnt++;q.insert(nn[i].r);
            }
        }
    }
    printf("%d\n",cnt);
    return 0;
}

G.Goblin Garden Guards 给n个哥布林的位置（x，y），给出m个圆，对于每一个圆，输出最大的不在圆内的哥布林数目。

由于哥布林的位置是整数，那么对于圆，可以预处理出距离圆心0~r范围内的x最大偏差值和y的最大偏差值，如果哥布林的x，y与圆心的偏差值有一者在最大偏差值之外，就cnt++。

#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm>
#define MOD 1000000007
using namespace std;
typedef long long ll;
struct point
{
    int x,y;
}p[100010];
bool cmp(point a,point b)
{
    return a.y<b.y;
}
vector<int>v[100010];
vector<int>d[110];
void init()
{
    for(int r=1;r<=100;r++)
        for(int i=0;i<=r;i++)
            d[r].push_back((int)floor(sqrt(1.0*r*r-i*i)));
}
int main()
{
    init();
    int g,m,x,y,r;
    scanf("%d",&g);
    for(int i=0;i<g;i++)
        scanf("%d%d",&p[i].x,&p[i].y);
    sort(p,p+g,cmp);
    for(int i=0;i<g;i++)
        v[p[i].x].push_back(p[i].y);
    scanf("%d",&m);
    int ans=0;
    for(int i=0;i<m;i++)
    {
        scanf("%d%d%d",&x,&y,&r);
        int left=max(0,x-r),right=min(10000,x+r);
        for(int dd=left;dd<=right;dd++)//横坐标
        {       
            int c=abs(dd-x);
            int yl=max(0,y-d[r][c]),yr=min(10000,y+d[r][c]);
            int pos1=lower_bound(v[dd].begin(),v[dd].end(),yl)-v[dd].begin();
            int pos2=upper_bound(v[dd].begin(),v[dd].end(),yr)-v[dd].begin();
            v[dd].erase(v[dd].begin()+pos1,v[dd].begin()+pos2);
            ans+=pos2-pos1;
        }
    }
    printf("%d\n",g-ans);
    return 0;
}

7.28 teemo场

A. Teemo’s bad day 裸的并查集，判断两个数字的根是否一样，不一样就cnt++，顺便union即可。（好久没写并查集find都写炸）

#include <bits/stdc++.h>
using namespace std;
int a[500010],b[500010];
int fa[100010];
int Find(int x)
{
    if(fa[x]==x)return x;
    return fa[x]=Find(fa[x]);
}
void Union(int p,int q)
{
    int rp=Find(p),rq=Find(q);
    if(rp!=rq)
        fa[rp]=rq;
}
void init(int n)
{
    for(int i=0;i<100010;i++)
        fa[i]=i;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n,cnt=0;
        scanf("%d",&n);
        init(n);
        for(int i=0;i<n;i++)
            scanf("%d",&a[i]);
        for(int i=0;i<n;i++)
        {
            scanf("%d",&b[i]);
            if(a[i]==b[i]) continue;
            if(Find(a[i])!=Find(b[i]))
            {
                cnt++;Union(a[i],b[i]);
            }
        }
        printf("%d\n",cnt);
    }
    return 0;
}

B. Teemo’s hard problem 题目意思是给你一个数列，你可以任意反转[L,R]，使得这个数列的非递减序列最长。

#include <bits/stdc++.h>
#define INF 0x3f3f3f3f3f3f3f3f
#define MOD 1000000007
using namespace std;
typedef long long ll;
int a[2010];
int pre[2010];//1的前缀长度（包括自己）
int suf[2010];//2的后缀长度（包括自己）
int dp[2005][2005][4];//[i,j]中以k结尾的最长非递增序列长度
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n;
        scanf("%d",&n);
        memset(pre,0,sizeof(pre));
        memset(suf,0,sizeof(suf));
        memset(dp,0,sizeof(dp));
        for(int i=1; i<=n; i++)
        {
            scanf("%d",&a[i]);
            if(a[i]==1)pre[i]=pre[i-1]+1;
            else pre[i]=pre[i-1];
        }
        for(int i=n; i>=1; i--)
        {
            if(a[i]==2)suf[i]=suf[i+1]+1;
            else suf[i]=suf[i+1];
        }
        for(int i=1; i<=n; i++)
        {
            dp[i][i][a[i]]=1;
            for(int j=i+1; j<=n; j++)
            {
                if(a[j]==1)
                {
                    dp[i][j][1]=max(dp[i][j-1][1],dp[i][j-1][2])+1;
                    dp[i][j][2]=dp[i][j-1][2];
                }
                else if(a[j]==2)
                {
                    dp[i][j][1]=dp[i][j-1][1];
                    dp[i][j][2]=dp[i][j-1][2]+1;
                }
            }
        }
        int ans=0;
        for(int i=1; i<=n; i++)
            for(int j=i; j<=n; j++)
            {
                ans=max(ans,pre[i-1]+max(dp[i][j][1],dp[i][j][2])+suf[j+1]);
            }
        printf("%d\n",ans);
    }
    return 0;
}

C. Teemo’s tree problem 又是一个dp

F. Teemo’s dream 没看题

G .Teemo’s convex polygon 将多边形对角线相连，其对角线最多被分割成多少段？
$$
max=(n^4-6n^3+17n^2-24*n)/12
$$
J. Teemo’s formula 结论是$Σ_{k=1}^nk^2C_n^k=2^{n-2}n(n+1)$

K.Teemo’s reunited 求的是其他所有的点到某一点的距离和的最小值，就是曼哈顿距离。HDU 4311Meeting point-1

这题也是用“分治”，虽说题目要求的是曼哈顿距离，但是我们为什么真的就要一步到位的求呢，可以横纵坐标分开求，先x排序，然后遍历一遍，求出横坐标的距离，然后y排序，遍历一遍求出坐标的距离加在刚才求得的x的距离上，就是曼哈顿距离了。

这里有一个非常巧妙但是其实很显而易见的东西：假定现在我们已经按x排好序了分别是ABC三个点，那么C到AB的距离和是|C-A|+|C-B|，又因为已经排序了，那么绝对值可以去掉，得(C-A)+(C-B)，那么就是2*C-(A+B)，也就是说一个点到它前面的点的距离的和等于它前面的点的个数乘以它的自己再减去前面所有点的和，到这里你是不是想到求一个数列的和的时候我们遍历一遍数列就得到了，通过这个方法我们用O(n)就得到了一个点到它前面的点的距离和，然后再倒着遍历一遍数列用相似的思想把它到它后面的点的距离再加上就行了。

还有一种也是分开x,y排序求和，不过可以这么做：先直接求出最前面的点到所有点的距离，然后依次遍历数列，通过后面一个点跟前面一个点的关系，找出差值相减，就是了。不明白的话仔细想想或者画图看看。

#include<iostream>
#include<cstring>
#include<algorithm>
#define INF 1000000000000007
using namespace std;
struct node{
	long long x,y;
	long long sum;
}a[100005];
bool cmp1(node a,node b)
{
	return a.x<b.x;
}
bool cmp2(node a,node b)
{
	return a.y<b.y;
}
int main(){
	int t,n;
	scanf("%d",&n);
	long long ans=INF;
	memset(a,0,sizeof(0));
	for(int i=0;i<n;i++)  
        scanf("%lld%lld",&a[i].x,&a[i].y);
	sort(a,a+n,cmp1);
	long long sum=0;
	for(int i=0;i<n;i++)
    {
		a[i].sum=i*a[i].x-sum;
		sum+=a[i].x;
	}
	sum=0;
	for(int i=n-1;i>=0;i--)
    {
		a[i].sum+=sum-(n-1-i)*a[i].x;
		sum+=a[i].x;
	}
	sort(a,a+n,cmp2);
	sum=0;
	for(int i=0;i<n;i++)
    {
		a[i].sum+=i*a[i].y-sum;
		sum+=a[i].y;
	}
	sum=0;
	for(int i=n-1;i>=0;i--)
    {
		a[i].sum+=sum-(n-1-i)*a[i].y;			
		sum+=a[i].y;
		ans=min(ans,a[i].sum);
	}
	printf("%lld\n",ans);
    return 0;
}

7.29

A. Coins 概率dp….不懂不懂

B. The Difference 水题

D. Fence Building 一个圆，一个圆的内接n边形，连接多边形对角线，求整个圆被分割成几块。

OEIS大法好。。。

#include<stdio.h>
#include<iostream>
#include<string.h>
#include<math.h>
#include<time.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<vector>
#include<cassert>
#include<algorithm>
#define INF 0x3f3f3f3f3f3f3f3f
#define MOD 1000000007
#define MAXN 10000000
using namespace std;
typedef long long ll;
void extgcd(ll a,ll b,ll d,ll &x,ll &y)   //a,b都为正整数
{
    if(b==0){d=a;x=1;y=0;}
    else{extgcd(b,a%b,d,y,x);y=y-x*(a/b);}
}
ll inverse(ll a,ll p)
{
    ll d,x,y;
    extgcd(a,p,d,x,y);
    return (x%p+p)%p;
}
int main()
{
    int t;
    ll n;
    scanf("%d",&t);
    for(int cs=1;cs<=t;cs++)
    {
        scanf("%lld",&n);
        n%=MOD;
        ll temp1=n,temp2=(temp1*n)%MOD,temp3=(temp2*n)%MOD,temp4=(temp3*n)%MOD;
        temp1=(temp1*18ll)%MOD,temp2=(temp2*23ll)%MOD,temp3=(temp3*6ll)%MOD;
        ll temp=inverse(24ll,MOD);
        //printf("%lld %lld %lld %lld %lld\n",temp1,temp2,temp3,temp4,temp);
        ll fz=(temp4-temp3+MOD)%MOD;
        fz=(fz+temp2)%MOD;
        fz=(fz-temp1+24+MOD)%MOD;
        ll ans=(fz*temp)%MOD;
        printf("Case #%d: %lld\n",cs,ans);
    }
    return 0;
}

G.The Mountain 水

I. A Possible Tree 给你一棵树，q个询问，问的是x->y路径上的异或和为val , 问你最多有几个询问是真的？

带权并查集。由于异或的特点，假设某个点为根，比如0，那么比如2->5的异或值，就是2->1的异或值和5->1的异或值异或一下。所以我们用yihuo[i]来表示i到源点的异或和。如果两个数的源点已经一样，那么判断一下val==yihuo[i]^yihuo[j]即可，若是不一样，就把他们union，同时yihuo[rootp]=yihuo[p]^yihuo[q]^val。

#include <bits/stdc++.h>
using namespace std;
int fa[100010],yihuo[100010];
int Find(int x)
{
    if(x!=fa[x])
    {
        int tmp=fa[x];
        fa[x]=Find(fa[x]);
        yihuo[x]^=yihuo[tmp];
        return fa[x];
    }
    return x;
}

bool Union(int p,int q,int val)
{
    int rp=Find(p),rq=Find(q);
    if(rp!=rq)
    {
        fa[rp]=rq;
        yihuo[rp]=yihuo[p]^yihuo[q]^val;
        return true;
    }
    if((yihuo[p]^yihuo[q])!=val)
        return false;
    return true;
}
void init(int n)
{
    for(int i=1;i<=n;i++)
    {
        fa[i]=i;yihuo[i]=0;
    }
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n,k,u,v,val;
        scanf("%d%d",&n,&k);
        init(n);
        for(int i=0;i<n-1;i++)
            scanf("%d%d",&u,&v);
        int flag=1,ans=0;
        for(int i=0;i<k;i++)
        {
            scanf("%d%d%d",&u,&v,&val);
            if(!Union(u,v,val)&&flag)
            {
                flag=0;
                ans=i;
            }
        }
        printf("%d\n",ans);
    }
    return 0;
}

K. Sum of the Line 给你一个n，分析之后发现求的是所有gcd(n,i)=1（i<=n）的数的平方和。

用容斥，先用公式$\frac{n(n+1)(2n+1)}{6}$求出1~n的平方和，然后筛出sqrt(n)内的素数，并求出n的所有质因数，然后对于质因数的乘积tot，如果质因数的个数是奇数，就加上$tot^2*(1^2+2^2+3^2……+(n/tot)^2)$，是偶数就减去。

或者用莫比乌斯反演来做

（补莫比乌斯反演做法）

#include<bits/stdc++.h>
#define INF 0x3f3f3f3f3f3f3f3f
#define MOD 998244353
#define MAXN 10000
using namespace std;
typedef long long ll;
ll pri[10010],num=0;
bool vis[10010];
vector<ll>pr;
void init()
{
    ll i,j;
    for(i=2;i<MAXN;i++)
    {
        if(vis[i]==false)pri[num++]=i;
        for(j=0;j<num&&i*pri[j]<MAXN&&i%pri[j]!=0;j++)
            vis[i*pri[j]]=true;
    }
}
void extgcd(ll a,ll b,ll d,ll &x,ll &y)
{
    if(b==0){d=a;x=1;y=0;}
    else{extgcd(b,a%b,d,y,x);y=y-x*(a/b);}
}
ll inverse(ll a,ll p)
{
    ll d,x,y;
    extgcd(a,p,d,x,y);
    return (x%p+p)%p;
}
int main()
{
    init();
    int t;
    ll n;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%lld",&n);
        pr.clear();
        ll xs=inverse(6ll,MOD);
        ll tot=(((n*(n+1))%MOD*(2*n+1))%MOD*xs)%MOD;
        ll temp=n;
        for(int i=0;i<num;i++)
        {
            if(temp%pri[i]==0)
            {
                pr.push_back(pri[i]);
                while(temp%pri[i]==0)
                    temp/=pri[i];
            }
        }
        if(temp>1)pr.push_back(temp);
        int len=pr.size();
        ll ans=0;
        for(int i=1;i<(1<<len);i++)
        {
            int cnt=0;//有几个1
            ll d=1;
            for(int j=0;j<len;j++)
            {
                int temp=i>>j&1;
                if(temp==1)
                {
                    cnt++;d=d*pr[j];
                }
            }
            ll gs=n/d;
            ll g=(((gs*(gs+1))%MOD*(2*gs+1))%MOD*xs)%MOD;
            if(cnt%2==0)ans=(ans-((d*d)%MOD*g)%MOD+MOD)%MOD;
            else ans=(ans+((d*d)%MOD*g))%MOD;
            }
        }
        printf("%lld\n",(tot-ans+MOD)%MOD);
    }
    return 0;
}

7.30 多校三

A. Problem A. Ascending Rating 输入n,m,k,p,q,r,MOD,表示一个长度为n的数列，给你前k个数字，（后面的要根据递推式自己写），然后m表示一个[l,l+m]的区间，从l=1开始，在这个区间中有两个值，一个是MAX，一个是CNT，起始都为0，从区间的第一个数开始扫，如果扫到的数字比MAX大，让MAX=ai，并且CNT++。求的是$A =\sum_{i=1}^{n-m+1}{MAX_i 异或i}$ , $B=\sum_{i=1}^{n-m+1}{CNT_i 异或i}$

思路是用一个单调队列从最后一个区间往前倒着维护，如果队列为空，则直接放入ai，若ai>=队首元素，则将队列中的元素全部弹出，同时将ai放入，若ai小于队首元素，则将队尾中小于ai的元素弹出，将ai放入队尾中，每一个区间的cnt值即为队列中元素的个数，而MAX值则为队首元素。如果队首元素的位置不在下一个区间范围内，则弹出。注意STL的双端队列会被卡，这里可以用数组直接模拟。（可以补一个正向写的，但是我WA到死，主要就是用单调栈来维护每一个数字右边的第一个比他大的位置，最后一个栈里的数的stack设为n+1，然后从右到左，dp[n-1]=1，dp[i]=dp[stack[i]]+1，………然后单调队列维护区间最大值）

#include <bits/stdc++.h>
using namespace std;
long long a[10000010];
long long que[20000010];
int main()
{
    int t,n,m,k,p,q,r,MOD;
    int size,front,rear;
    scanf("%d",&t);
    while(t--)
    {
        size=0;
        front=rear=1e7+5;
        scanf("%d%d%d%d%d%d%d",&n,&m,&k,&p,&q,&r,&MOD);
        for(int i=1;i<=k;i++)
            scanf("%lld",&a[i]);
        for(int i=k+1;i<=n;i++)
            a[i]=(1LL*p*a[i-1]+1LL*q*i+r)%MOD;
        long long MAX=0,CNT=0;
        for(int i=n;i>=1;i--)
        {
            if(size==0)
            {
                que[front]=i;size=1;
            }
            else
            {
                if(a[que[front]]<=a[i])
                {
                    front=rear=1e7+5;
                    que[front]=i;
                    size=1;
                }
                else
                {
                    while(size>0&&a[que[rear]]<=a[i])
                        size--,rear--;
                    que[rear+1]=i;rear++;
                    size++;
                }
            }
            if(i<=n-m+1)
            {
                MAX+=a[que[front]]^i;
                CNT+=size^i;
                while(que[front]>=(i+m-1))
                    front++,size--;
            }
        }
        printf("%lld %lld\n",MAX,CNT);
    }
    return 0;
}

C. Problem C. Dynamic Graph Matching 在一个图中，任意k条不共点的边可以构成一个匹配。给你n个点，有q个操作，操作分两种，一种是+ u v，在u v中间连线，一个是- u v，删边，两点之间可以连多条路线。问你对于每一次操作，k=1,2，…… n/2的匹配方案分别有多少？

思路：树状DP。（补）

D. Problem D. Euler Function 水。求φ(n)为合数的第k个数。根据规律可看到，从第7个开始就都是偶数。

F. Problem F. Grab The Tree 水。很容易看出sum=0时平手，否则就是先手赢。

L. Problem L. Visual Cube 水。直接写。

7.31 ACM-ICPC 2015 Shenyang Preliminary C…

B. Best Solver （补）

C. Minimum Cut （补）

F. Fang Fang 水。

J. Jesus Is Here 有、搞的题。把递推关系算出来……表示不想再写一编代码，就那个意思反正。

#include<bits/stdc++.h>
using namespace std;
#define MOD 530600414
typedef long long ll;
ll sum[210000];
ll num[210000];
ll pre[210000],suf[210000],ans[210000];
void init()
{
    sum[1]=5;sum[2]=8;num[1]=1;num[2]=2;
    for(int i=3;i<=201314;i++)
    {
        sum[i]=(sum[i-1]+sum[i-2])%MOD;
        num[i]=(num[i-1]+num[i-2]+1)%MOD;
        if(i%2==1)sum[i]=(sum[i]+5)%MOD;
        else sum[i]=(sum[i]+3)%MOD;
    }
    pre[1]=5;pre[2]=11;suf[1]=5;suf[2]=13;
    for(int i=3;i<=201314;i++)
    {
        ll x;
        if(i%2==1)x=5;else x=3;
        pre[i]=((((num[i-1]+1)*(sum[i-2]+x))%MOD+pre[i-2])%MOD+pre[i-1])%MOD;
        suf[i]=((((num[i-2]+1)*(sum[i-1]+x))%MOD+suf[i-2])%MOD+suf[i-1])%MOD;
    }
    ans[1]=5;ans[2]=16;
    for(int i=3;i<=201314;i++)
    {
        ll x;
        if(i%2==1)x=5;else x=3;
        ll temp1=((num[i-1]+1)*suf[i-2])%MOD;
        ll temp2=((num[i-2]+1)*pre[i-1])%MOD;
        ll temp3=(((num[i-1]+1)*(num[i-2]+1))%MOD*x)%MOD;
        ans[i]=((((temp1+temp2)%MOD+temp3)%MOD+ans[i-2])%MOD+ans[i-1])%MOD;
    }
}
int main()
{
    init();
    int t,n;
    scanf("%d",&t);
    for(int kase=1;kase<=t;kase++)
    {
        scanf("%d",&n);
        if(n<5)printf("0\n");
        else
        {
            n-=4;
            printf("Case #%d: %lld\n",kase,ans[n]);
        }
    }
    return 0;
}

M. Largest Point 写的我脑子有点不清楚了……

8.1多校4

B. Harvest of Apples 题意是从n个苹果里面选取最多m个苹果的方案数量。m、n、t<=1e5

思路：莫队分块+组合预处理，原来莫队中的区间[l,r]在这里用n、m代替了。

接下来是推公式部分：

S(n,m)表示$\sum_{i=1}^n\sum_{j=1}^mC_i^j$

我们可以得出$S(n,m)=S(n,m-1)+C_n^m$ ,——-①

又因为有$C_n^m=C_{n-1}^m+C_{n-1}^{m-1}$（组合数学的一个基本公式），因此又可以推出：$S(n,m)=S(n-1,m)+S(n-1,m-1)=2S(n-1,m)-C_{n-1}^m$——–②

有了①②两个式子，我们就可以得到S(n,m)和S(n-1,m)、S(n+1,m)、S(n,m-1)、S(n,m+1)之间的关系，先预处理出n！和相应的需要的逆元，然后把输入的查询分块，按照代码中所示的“套路”排序法，排一排，然后对于每个n，m开始处理，分四种情况这样。

#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
const long long MOD =1e9+7;
typedef long long ll;
ll multi[N];
ll devide[N];
ll ans[N];
ll pos[N];
ll er;
int D=(int)sqrt(1.0*N);
struct node{
    int n,m;
    int id;
    bool operator <(const node& p) const{
        if(pos[n]==pos[p.n]) return m<p.m;
        return n<p.n;                           //N大的排前面
    }
};
node qujian[N];
ll ex_gcd(ll a,ll b,ll &x,ll &y)//扩展欧几里得（扩展gcd）
{
	if (a==0&&b==0) return -1;
	if (b==0){x=1;y=0;return a;}
	ll d=ex_gcd(b,a%b,y,x);
	y-=a/b*x;
	return d;
}

ll mod_inverse(ll a,ll n)//乘法逆元,n取模
{
	ll x,y;
	ll d = ex_gcd(a,n,x,y);
	return (x%n+n)%n;
}

void init(int n)
{
    multi[0]=1;
    multi[1]=1;
    for(int i=2;i<=n;i++)
        multi[i]=multi[i-1]*i%MOD;
    devide[n]=mod_inverse(multi[n],MOD);
    for(int i=n-1;i>=0;i--)
        devide[i]=devide[i+1]*(i+1)%MOD;
}
ll cal(int n,int m)
{
    return ((multi[n]*devide[m])%MOD*devide[n-m])%MOD;
}
void operation1(int n,int m,ll &res)
{
    res=((2ll*res)%MOD-cal(n,m)%MOD+MOD)%MOD;
}
void operation2(int n,int m,ll &res)
{
    res=(res+cal(n-1,m))%MOD*er%MOD;
}
void operation3(int n,int m,ll &res)
{
    res=(res+cal(n,m+1))%MOD;
}
void operation4(int n,int m,ll &res)
{
    res=(res-cal(n,m)+MOD)%MOD;
}
int main()
{
    init(100000);
    int t;
    int n,m;
    er=mod_inverse(2ll,MOD);
    scanf("%d",&t);
    for(int i=1;i<=t;i++)
    {
        scanf("%d%d",&qujian[i].n,&qujian[i].m);
        qujian[i].id=i;
        pos[i]=i/D;
    }
    sort(qujian+1,qujian+t+1);
    int curl,curr;
    curl=curr=1;
    ll res=2;
    for(int j=1;j<=t;j++)
    {
        while(curl<qujian[j].n) operation1(curl++,curr,res);
        while(curr<qujian[j].m) operation3(curl,curr++,res);
        while(curl>qujian[j].n) operation2(curl--,curr,res);
        while(curr>qujian[j].m) operation4(curl,curr--,res);
        ans[qujian[j].id]=res;
    }
    for(int i=1;i<=t;i++)
        printf("%lld\n",ans[i]);
    return 0;
}

D. Nothing is Impossible 水，按占比来算就好。

E. Matrix from Arrays 讲一下思想吧，再写一边代码的话可能又要写一万年。对于这个块的计算，比如这个块的四个角顺时针分别叫：a,b,c,d，将(0,0)点到(i,j)点的里面所有的数字和叫做pre，那么就是pre[b]-pre[b]-pre[d]+pre[a]。分析一下就可以得到，对于所有的无限大的矩阵，他都是重复某个特定的矩阵来的。这些矩阵有以下长度规律：（L为给定数组的长度，L从1~10，）

len[1]=1,len[2]=4,len[3]=3,len[4]=8,len[5]=10,len[6]=12,len[7]=14,len[8]=16,len[9]=18,len[10]=20。

矩阵为n*n。

故对于给定的L和数组可以先处理出重复矩阵的样子，然后再进行分块和的计算。

关于分块和的计算（pre），把块内完整的小矩阵的个数算出来求个和，除了完整的还有不完整的，不完整的其实也好看，就是矩阵最左边和最上面的部分，也用pre算出来就行。

J. Let Sudoku Rotate 数独，有一个16*16的数独数独内的数字从0~E，一开始数独是完美的，可是有个人逆时针旋转了数独中的某几块（4x4），导致数独不完美了，给你这个旋转后的数独，要求还原他至少要再旋转几步？

dfs+剪枝。

写出下列几个操作：

顺时针旋转4*4的方块；
判断每行的总和是否都为120；
判断每行和每列的元素是否都不重复；
dfs，由于一行块有4个分块，因此四重循环，同一个x分别对应y的起始：0，4，8，12，循环+1表示旋转次数+1，如果在2、3的判断中都满足这写要求，说明可以进行下一个x+4（起始行）块的旋转操作dfs，step+本次旋转的操作（i，j，k，l四重循环），要是不满足还是要继续。当x==16或者是step比当前已知的最小ans要大的时候都可以return。

#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
const int INF = 0x3f3f3f3f;
const long long MOD =1e9+7;
typedef long long ll;
char m[20][20];
char cop[4][4];
int ans=64;
void print()
{
    printf("\n");
    for(int i=0;i<16;i++,printf("\n"))
        for(int j=0;j<16;j++)
            printf("%c",m[i][j]);
    printf("\n");
}
int rol(int x,int y)
{
    for(int i=0;i<4;i++)
        for(int j=0;j<4;j++)
            cop[i][j]=m[x+3-j][y+i];
    for(int i=0;i<4;i++)
        for(int j=0;j<4;j++)
            m[i+x][j+y]=cop[i][j];
}
bool sum(int x)
{
    for(int j=x;j<x+4;j++)
    {
        int temp=0;
        for(int i=0;i<16;i++)
        {
            temp=temp+((m[x][i]>='0'&&m[x][i]<='9')?(m[x][i]-'0'):(m[x][i]-'A'+10));
        }
        if(temp!=120) return false;
    }
    return true;
}
bool multi(int x)
{
    int vis[16]={0};
    for(int j=x;j<x+4;j++)
    {
        memset(vis,0,sizeof(vis));
        for(int i=0;i<16;i++)
        {
            int temp=((m[j][i]>='0'&&m[j][i]<='9')?(m[j][i]-'0'):(m[j][i]-'A'+10));
            vis[temp]++;
            if(vis[temp]>1) return false;
        }
    }

    for(int i=0;i<16;i++)
    {
        memset(vis,0,sizeof(vis));
        for(int j=0;j<=x+3;j++)
        {
            int temp=((m[j][i]>='0'&&m[j][i]<='9')?(m[j][i]-'0'):(m[j][i]-'A'+10));
            vis[temp]++;
            if(vis[temp]>1) return false;
        }
    }
    return true;
}
void dfs(int x,int step)
{
    if(step>ans) return;
    if(x==16)
    {
        ans=min(ans,step);return;
    }
    for(int i=0;i<4;i++,rol(x,0))
    for(int j=0;j<4;j++,rol(x,4))
    for(int k=0;k<4;k++,rol(x,8))
    for(int l=0;l<4;l++,rol(x,12))
    {
        if(!(sum(x)&&multi(x))) continue;
        dfs(x+4,step+i+j+k+l);
    }
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        getchar();
        for(int i=0;i<16;i++)
            scanf("%s",m[i]);
        ans=64;
        dfs(0,0);
        printf("%d\n",ans);
    }
    return 0;
}

K. Expression in Memories 表达式中有一些是用？代替的，问你这个表达式能否符合正确的要求，能的话输出任意成立的表达式（不含？）。注意细节，一开始对“+0?”单独扫，？填运算符号。完了之后就按顺序扫，判断是否符合。（注意细节，容易wa）

#include <bits/stdc++.h>
using namespace std;
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        string a;
        cin>>a;
        int flag=1;
        int len=a.size();
        for(int i=2;i<len;i++)
        {
            if(a[i]=='?'&&a[i-1]=='0'&&(a[i-2]=='+'||a[i-2]=='*'))
                a[i]='+';
        }
        for(int i=0;i<len&&flag;i++)
        {
            if(a[i]=='?') {a[i]='1';continue;}
            if(a[i]=='+'||a[i]=='*')
            {
                if(i==len-1||i==0) flag=0;
                else if(a[i+1]=='+'||a[i+1]=='*') flag=0;
            }
            else if(a[i]=='0')
            {
                if(i==0&&len>1&&(a[i+1]!='+'&&a[i+1]!='*'&&a[i+1]!='?')) {flag=0;continue;} 
                if((i-1)<0||a[i-1]=='+'||a[i-1]=='*') 
                    if(i+1<len)
                    {
                        if(a[i+1]=='?') a[i+1]='+'; 
                        else if(a[i+1]!='+'&&a[i+1]!='*') flag=0;
                    }
            }
        }
        if(!flag)
            printf("IMPOSSIBLE\n");
        else
            cout<<a<<endl;
    }
    return 0;
}

L. Graph Theory Homework 水，得到结论：根号函数的性质：$\sqrt{a+b+c+…}\le\sqrt{a}+\sqrt{b}+\sqrt{c}+…$