容斥
公式
$$
|A_1∪A_2∪…∪A_n|=\sum_{i=1}^n|A_i|-\sum_{i=1}^n\sum_{j>i}|A_i∩A_j|+\sum_{i=1}^n\sum_{j>i}\sum_{k>j}|A_i∩A_j∩A_k|+…
$$
$$
+(-1)^{n-1}|A_1∩A_2∩…∩A_n|
$$
应用
错排问题
棋盘多项式与有禁区的排列
布棋问题
一个n*m棋盘上放k个棋子,其中任意两个棋子不能位于同一行或者同一列上。问种数。
布棋方案数 $R_k(C)$ : k个棋子依照上述规则放在棋盘C中的方案数
棋盘多项式: 棋盘C中放不限定数量的棋子,$R(C)=\sum_{k=0}^∞R_k(C)x^k$(有点母函数的味道),由于k<=C(格子数),因此这个多项式也是有限的。
放置: $R_k(C)=R_{k-1}(C_x)+R_k(C_e)$
C表示这个棋盘,$C_x$表示放在棋盘C除去这个格子所在的行和列之后的棋盘,$C_e$表示棋盘C删去这个格子后的棋盘。
那么这个公式的意思就是,在棋盘C上放k个棋子的种数,等于(第k个棋子放在一个格子上,前k-1个数量的格子放在除了这个格子所在的行和列的地方),加上,(k个棋子放在除了这个格子的其他地方)。
棋盘多项式性质:
- $R(C)=xR(C_x)+R(C_e)$
- 若C由两个互不干扰的棋盘组成,有$R(C)=R(C_1)·R(C_2)$

有禁区的排列
排列数定理:
$$
n!-r_1(n-1)!+r_2(n-2)!-…±r_n
$$
$r_i$表示有$r_i$个棋子布置到禁区的方案数。(**仅适用n·n的棋盘**)
< 例题 > 有1,2,3,4号工人,A,B,C,D四个人物,1号不做B,2号不做B、C,3号不做C、D,4号不做D,问有多少种分配方式?
【解】先构造一个4*4的棋盘,然后画出这个棋盘的禁区,对于这个禁区计算它的棋盘多项式,得$R(C)=1+6x+10x^2+4x^3$,因此用容斥的思想,得到:
$$
4!- 6·(4-1)!+10·(4-2)!-4·(4-3)! +0(4-4)!= 4
$$
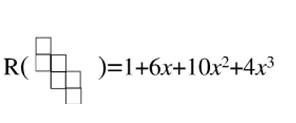
鸽巢定理
基本定理
n+1只鸽子飞回n个鸽巢,至少有一个鸽笼含有不少于2只的格子。
数学描述:
m($1\le m$)个元素分成n个组,那么总有一个组至少含有元素个数$\lceil\frac{m}{n}\rceil$
小应用
对于正整数序列,$a_1,a_2,…,a_m$,至少存在整数k和l, $1\le k<l\le m$,使得$a_k+a_{k+1}+…+a_l$是m的倍数。
【证明】对每个元素$a_i$构造一个前缀和sum[i],则有两种可能性:
(1) 若有一个sum[i]是m的倍数,则证毕;
(2) 若没有一个sum[i]为m的倍数,则令$r_h\equiv S_h mod\ m $ 。
其中,h=1,2,…,m,我们已知上面所有的项都非m的倍数,故余数r[i]的范围在[1,m-1],共m个数,根据鸽巢定理,m个余数在[1,m-1]共m-1的范围内至少存在一对$r_h$,$r_k$,满足$r_k=r_h$,则sum[k]和sum[h]满足:
$$
S_k\equiv S_h mod \ m
$$
设h>k的话,得到
$$
S_h-S_k=(a_1+a_2+…+a_h)-(a_1+a_2+…+a_k)
=a_{k+1}+…+a_h\equiv 0\ mod \ m
$$
证毕。中国剩余定理
