总体
用户设备会将任务分发到移动边缘计算服务器上,但是在offload过程中,由于小基站的高干扰、多址、资源有限,需要一种高效的计算卸载方案。在这篇论文中,作者研究了在小型蜂窝网络下的边缘计算系统的节能计算卸载方案,通过计算卸载决策、信道、传输功率和计算资源的联合优化,为的就是减少所有终端设备的能耗。终端设备不仅要决策是否卸载,也要决策卸载到哪里。
文章首先给出了计算卸载模型,并将此问题表述为一个NP难的混合整数非线性规划问题。利用遗传算法和粒子群优化算法,设计了一个次优算法——分层遗传算法(hierarchical GA)和基于粒子群算法(PSO-based computation)的计算算法。最后通过仿真研究了收敛性,并与其他基准算法比较,验证了它的性能。
简单介绍
移动边缘计算中,计算卸载是关键环节,包含:传输过程、远程执行过程、结果回传过程。通过网络将计算卸载到边缘计算服务器中,大大降低时延,延长设备使用。
该团队解决了三个挑战:计算决策、无线资源分配、计算资源分配。
计算决策问题
决定计算任务要在云端还是用户设备端进行。虽然边缘服务器可以为设备提供云服务,但是无法保证所有的设备在有限的网络和计算能力下都能得到服务。或者是过量的任务卸载到边缘,会造成拥塞、用户间交流的高干扰。
——通过优化多用户间多小区网络中的计算决策问题、平衡用户服务和系统收益。
无线资源分配
能耗是很重要的一部分。由于UE与边缘服务器的通信距离相对短,可以降低能耗。但是计算卸载的能效依赖于无线资源分配方案。传输功率增加,数据速率增加,但干扰和传输能耗也增加,延迟也可能增加。因此分配无线资源时,需要更高效的干扰管理方案,自适应的功率控制。
计算资源分配
应该不均匀分配。1)不同用户有不同的任务大小;2)根据网络状况的良莠,QoS需要更多/更少的计算资源
联合动态无线和计算资源分配方案。
考虑多个SBS服务多个用户的MEC系统,考虑干扰管理、功率控制方案,优化卸载决策、信道分配、计算资源分配方案来研究节能计算方案。工作:
- 提出采用MEC的分布式SCN的计算卸载系统模型,MBS与SBS都配备了MEC服务器。从延迟和能耗方面给用户带来好处,给系统的效率提升。
- 在边缘计算系统中,将能耗计算卸载问题定义为一个混合整型非线性编程问题(MINLP)——NP-hard。主要就是为例如在满足所有用户设备的异构质量服务要求和资源分配原则下,以最少的能耗完成任务。
- 基于层次GA、PSO,提出HGPCA次优化算法。提高收敛速度和性能。并分析算法的复杂性和收敛性。
- 模拟时,部署了数百个用户和数十个小基站,研究算法收敛性并与其他基准算法比较验证性能。
系统模型
A. 小型蜂窝网络下的移动边缘计算系统
| 变量 | 意义 | 中文 |
|---|---|---|
| $$N_B={0,1,2,…i,…,N}$$ | SBS | 基站 |
| $$u={1,2,…,j,…,U}$$ | UEs | 用户终端 |
| $$T_j={d_j,X_j,T^{max}_j}$$ | Task | j的计算任务 |
- 每个UE都有一个非密集型计算任务需要完成。

SBS与UE随机分配在MBS周围
计算任务j:
$$
T_j={d_j,X_j,t^{max}_j}
$$
| 变量 | 意义 |
|---|---|
| $$d_j$$ | 计算需要上传的数据 |
| $$X_j$$ | 处理1位输入需要的CPU周期数,每个任务都不同 |
| $$t^{max}_j$$ | 任务能接受的最大时延 |
| $$f_j=d_jX_j$$ | 完成第j个计算任务需要的CPU周期数 |
- 每个任务可以在本地计算,也可以卸载到MBS或SBS中的MEC服务器。
- 卸载需要三步:1)通过无线信道上传数据;2)在MEC服务器上执行任务;3)从MEC服务器上下载结果到UE。【重点放在前两步,涉及到一个通信模型和一个计算模型】
B. 通信模型
主要集中在上行链路传输。
| 变量 | 意义 | |
|---|---|---|
| $$a^{(i)}_j\in{0,1}$$ | 任务j是否卸载、卸载到哪个基站 | 0:不卸载,1:卸载 |
| $$A={a^{(i)}_j,i\in N_B,j\in u}$$ | 决策profile | |
| $$\sum_{i\in N_B}a^{(i)}_j \le1$$ | 终端j的任务只能被一个基站处理 | |
| $$c={1,2,…,k,…,C}$$ | 信道们 | |
| $$c_M={1,2,…,C_M}$$ | MBS的信道 | |
| $$c_S={C_M+1,C_M+2,…,C}$$ | SBS的信道 | $C-C_M=\rvert c_S\rvert$ |
| $$W$$ | 每个信道的带宽 | 每个信道都是独立同分布的 |
- 假设MBS与SBS使用不同的无线电频谱来避免层间干扰。对于SBS,频谱以叠加的方式使用时,意味着在小区之间存在干扰。而每个信道是正交的,也就是说同一个区内,不存在干扰。
- MaUs :UE的任务被大型基站处理
- SUs :UE的任务被小型基站处理
| 变量 | 意义 | |
|---|---|---|
| $$b^{(k)}_j\in{0,1}$$ | 信道分配指示器 | 信道k分配给UE-j |
| $$B={b^{(k)}_j,j\in u,k\in c}$$ | 信道分配指示profile | 满足1)2)条件 |
| $$\sum_{i\in N_B}\sum_{k\in{c_a}}a^{(i)}_jb^{(k)}_j\le1$$ | 每个基站的一个信道最多只能分配给给一个任务 | 1) |
| $\sum_{j\in u}\sum {k\in c_a}a^{(i)}_jb^{(k)}_j\le\rvert c_a\rvert$ | 分配给所有终端的信道不能超过每个BS中的信道总数。 | 2) |
| $$c_a$$ | 一些基站中可得到的信道集合 | 对于SBS来说$c_a=C_S$,对于MBS来说$c_a=C_M$ |
- 假设所有终端在传输时它的传输功率是静态的。
| 变量 | 意义 |
|---|---|
| $$p_j$$ | 终端j的传输功率 |
| $$P={p_1,…,p_j,…,p_U}$$ | 终端传输功率集profile |
| $$p_{max}$$ | 最大传输功率 |
传输速率R_0
当满足$a_{j}^{(0)}=1$时,UE-j分配得信道k ($b_j^{(k)}=1$),则传输速率R满足:
$$
R^{0}j(A{_j},B,P)=\sum_{k\in{c_a}}b^{(k)}jWlog_2(1+\frac{p_j\rvert h{0j}^{(k)}\rvert^2}{N_0})
$$
- $A_{_j}$是除了UE-j外的卸载决策profile
- $h_{0j}^{(k)}$是从UE-j到MBS的信道增益系数(2信道增益、比值信噪比)
- $N_0$是复高斯白噪声方差
小区间干扰指示函数$\delta$
考虑相邻的SBS中的SU-j‘对该SU-k信道接收信号的干扰,将小区间干扰指示函数表示为:
$$
\delta_{i,j^{‘}}^{(k)}=\begin{cases}
1,RSS_{i,j^{‘}}^{(k)} \ge RSS_{th}\
0,else.
\end{cases}
$$
$$
RSS_{i,j^{‘}}^{(k)} = \sum_{i^{‘}\in{N_B}\setminus i}
a^{(i{‘})}{j{‘}}b^{(k)}{j{‘}}p_{j{‘}}
\rvert h^{(k)}_{i,j{‘}}\rvert^2
$$
RSS表示SU-j’ 对SBS-i的分配信道k上的干扰功率,RSSth表示干扰阈值;su-j’和SBS-i不相关。
| 变量 | 意义 |
|---|---|
| $$RSS_{i,j^{‘}}^{(k)}$$ | $SU-j’$ 在$SBS-i$ 分配的信道$k$上收到的干扰功率 |
| $$RSS_{th}$$ | 干扰阈值 |
| $SU-j’$ 与$SBS-i$ 不相关 |
来自其他SU对SBS-i的信道k的干扰I
来自其他SU对SBS-i、信道k的干扰:
$$
I_{ij}^{(k)}(A_{_j},B_{_j},P_{_j})=
\sum_{i’\in N_B\setminus 0}
\sum_{j’\in u\setminus j}
a_{j’}^{(i’)}b^{(k)}{j’}
\delta{i,j^{‘}}^{(k)}
p_{j’}\rvert h_{i,j’}^{(k)}\rvert^2
$$
| 变量 | 意义 |
|---|---|
| $$B_{_j}$$ | 除了UE-j外的信道分配指示集 |
| $$P_{_j}$$ | 除了UE-j外的传输功率集 |
| $$h_{i,j’}^{(k)}$$ | 在SBS-i和UE-j’之间的信道k的信道增益系数 |
传输速率R_i
故,达到的传输速率:
$$
R^i_j(A_{_j},B,P)=
\sum_{k\in c_a}
b^{(k)}j Wlog_2
(1+\frac
{p_j\rvert h{ij}^{(k)}\rvert^2}
{I^{(k)}{ij} (A{_j},B_{_j},P_{_j})+N_0})
$$
C. 计算模型
计算任务是如何在本地终端的UE上执行的,或者是在MEC服务器上远程执行。
1)本地计算
假设每个终端的CPU在计算时的频率不变,但不同的终端可能有不同的频率。
| 变量 | 意义 | |
|---|---|---|
| $$F_j^{(l)}$$ | 每个终端UE-j的计算能力 | 通过CPU周期表示(Hz/s) |
| $$p^{(e)}_{j,l}$$ | 终端UE-j本地计算时CPU一个周期的能耗 |
终端本地计算的延迟T
$$
T^{(e)}_{j,l}=\frac
{f_j}
{F_j^{(l)}}
$$
本地计算的能耗E
$$
E_{j,l}^{(e)}=f_jp^{(e)}_{j,l}
$$
2)边缘计算
BS 传输的延迟T(第一阶段)
$$
T_{j,off}^{(i,tr)}(A_{_j},B,P)=\frac
{d_j}
{R_j^{(i)}(A_{_j},B,P)}
,i \ge0
$$
BS 传输能耗E(第一阶段)
$$
E_{j,off}^{(i,tr)}(A_{_j},B,P)=
P_jT_{j,off}^{(i,tr)}(A_{_j},B,P)
$$
| 变量 | 意义 | |
|---|---|---|
| $$F_i (i\in N_B)$$ | 每个BS的计算能力 | $F_0 \gg F_i,i>0$,大型基站的计算能力要远远大于小型基站 |
| $$F_j^{(i)}$$ | UE=j分配到的MEC-i的计算资源 | |
| $$F={F_j^{(i)},i\in N_B,j\in u }$$ | 计算资源的分配集profile | $\sum_{j\in u}F_j^{(i)} \le F_i,\forall i\in N_B $,即对于分配给终端j的资源,必须小于等于基站i的总资源 |
边缘计算时延
$$
T_{j,off}^{(i,e)}(F)=\frac{f_j}{F_j^{(i)}}
$$
忽略MEC上执行任务的能耗,因为BS能源丰富。另外也不考虑第三阶段,因为实际情况,传入数据往往比输出的数据要大。
总时延T
$$
T_j^{(i,off)}(A_{_j},B,P,F)=
T_{j,off}^{(i,tr)}(A_{_j},B,P)+
T_{j,off}^{(i,e)}(F)
$$
总能耗E
$$
E_j^{(i,off)}(A_{_j},B,P)=E_{j,off}^{(i,tr)}(A__j,B,P)
$$
问题公式化和分析
在该系统模型的基础上,将计算卸载问题定义为一个优化问题,包括计算卸载决策、无线资源管理、功率控制和计算资源分配。然后对所述问题进行了复杂性分析。
A. 问题表示
对于A、B、F,可以得到完成UE-j任务的时延和能耗
完成任务的时延
$$
T_j(A,B,P,F)=
\sum_{i \in N_B}a_j^{(i)}T_j^{(i,off)}
(A_{_j},B,P,F)+(1-\sum_{i\in N_B}a_j^{(i)})
T_{j,l}^{(e)}
$$
完成任务的能耗
$$
E_j(A,B,P,F)=
\sum_{i\in N_B}a_j^{(i)}E_j^{(i,off)}(A_{_j},B,P)+
(1-\sum_{i\in N_B}a_j^{(i)})E_{j,l}^{(e)}
$$
当满足$a_j^{(i)}=0$时,有$T_j^{(i,off)}=0,E_j^{(i,off)}=0$
问题$P_0$
求最小的所有终端总能耗
$$
P_0: \min_{A,B,P,F} \sum_{j\in u}E_j(A,B,P,F)\
$$
| 序号 | 公式条件 | 意义 |
|---|---|---|
| C1 | $$T_j(A,B,P,F)\le t_j^{max},\forall j\in N_u$$ | 所有UE的时延 |
| C2 | $$\sum_{j\in u}\sum_{k\in c_a}a_j^{(i)}b_j^{(k)}\le\rvert c_a\rvert$$ | 分配的信道之和不能超出可分配量 |
| C3 | $$\sum_{j\in u}F_j^{(i)}\le F_i,\forall i\in N_B$$ | 分配的计算资源不能超过该基站所有资源 |
| C4 | $$\sum_{i\in N_B}a_j^{(i)}\le 1,\forall j \in u$$ | 一个任务只能卸载到一个基站 |
| C5 | $$\sum_{i\in N_B}\sum_{k\in c_a} a_j^{(i)}b_j^{(k)} \le 1, \forall j\in u$$ | 一个信道只同时被一个终端使用 |
| C6 | $$a_j^{(i)}\in {0,1},\forall i\in N_B,j\in u$$ | 每个UE任务j是否卸载到BS-i |
| C7 | $$b_j^{(k)}\in {0,1}, \forall i\in N_B,j\in u,k\in c$$ | 每个UE-j是否使用信道k |
| C8 | $$0\le F_j{(i)}\le F_i,\forall i\in N_B,j\in u$$ | UE-j从BS-i分配到的计算资源不能超过BS-i总量 |
| C9 | $$0\le p_j\le p_{max},\forall j \in u $$ | UE-j的传输功率小于最大功率 |
| C10 | $$a_j^{(i)}=\sum_{k\in c_a}b_j^{(k)} = I(F_j^{(i)}),\forall i\in N_B,j\in u$$ | |
| $$I(·)=\begin{cases}1,·>0\ 0,otherwise\end{cases}$$ | 指示器,避免一个终端只分配到计算资源或无线资源下的资源浪费 |
B. 问题分析
目标
$P_0$旨在求得所有终端最小的总能耗,通过优化卸载决策A,信道分配指示B,传输功率P,计算资源分配指示F。
NP难问题——混合整数非线性编程问题(MINLP)A,B中是二进制变量,P、F中是正实数。$P_0$问题非光滑、非微分或连续。
拟议算法
| Algorithm1 HGPCA(基于粒子群PSO和分层遗传算法GA) |
|---|
| 1. input : 种群个体数量K,HGPCA的迭代T次数,收敛准则$\epsilon$,GA的参数交叉和突变的概率$p_m,p_c,T_1$,PSO的参数$w,c_1,c_2,T_2$ |
| 2. output : 在T此迭代后的K个个体,和历史中的适应度值最佳的值 |
| 3. 初始化 : 用表达式(18)初始化K个个体,让$t=0$ |
| 4. Step 1 : if $t>T$ or $Fitness(t)-Fitness(t-1)\le\epsilon$,break;else,go to Step 2. |
| 5. Step 2 : 执行 Algorithm 2 |
| 6. Step 3: 执行 Algorithm 3 |
| 7. Step 4: $t=t+1$, go to Step 1 |
A. HGPCA 流程
GA——优胜劣汰,适合大范围搜索,收敛速度慢(基础)
PSO——适合局部搜索,收敛快,易陷入局部最优(优化)
在每一次迭代时,先用GA作为T1迭代,得到粗粒度的结果,然后用T1的结果传入PSO作为T2的迭代,下一次迭代的输入,就是T2的迭代输出。当$t=0$时,用表达式(17)作为input。
| Algorithm 2 底层GA |
|---|
| 1. Input : 种群中$K$个个体,$p_m,p_c$,GA $T_1$ 迭代次数 |
| 2. Output : 经过$T_1$迭代后的$K$个种群,以及最优值 |
| 3. Step 1 : if $t_1 > T_1$, break; else, go to Step 2. |
| 4. Step 2 : 评估种群,即计算个体的适应度值 |
| 5. Step 3 : 找到本次迭代中最优的个体$I_{best}^{t_1}$,并记录在历史最优上$H_{best}$。if $I_{best}^{t_1}$ is better than $I_{best}$,$I_{best}=I_{best}^{t_1}$,else $I_{best}=I_{best}^{t_1-1}$。 |
| 6. Step 4 : 根据设定的规则选择$K$个个体,另外,如果$I_{best}$不在父集上,就用$I_{best}$代替坏的个体。另外,选择两个不可行的个体保留。 |
| 7. Step 5 : 随机选择两个个体,并以交叉概率$p_c$进行交叉操作 |
| 8. Step 6 : 对于每个个体,以突变概率$p_m$进行突变操作 |
| 9. Step 7 : $t_1=t_1+1$,go to Step 1 |
| Algorithm 3 上层PSO |
|---|
| 1. Input : 由算法2生成的精英粒子$\kappa$,蜂群的大小$K$,PSO的迭代次数$T_2$,PSO的参数$w,c_1,c_2$ |
| 2. Output : 在$T_2$迭代后的粒子,以及历史最优值 |
| 3. 初始化 : 初始化精英粒子$\kappa$的速度,设置迭代次数$t_2=0$,计算每个粒子的最优值 |
| 4. Step 1 : if $t_2 > T_2$,break;else,go to Step 2 |
| 5. Step 2 : 根据表达式(22)和(23)更新粒子$\kappa$的速度$V_k^{t_2}$和位置$X_k^{t_2}$,找到历史最优粒子 |
| 6. Step 3 : 评估迭代中每个粒子的适合度值。对于每个粒子,如果它的新适应度比自己的最佳适应度$p_{best}$要好,就更新 |
| 7. Step 4 : 找到所有粒子中基于每个粒子$p_{best}$的最优值$g_{best}$ |
| 8. Step 5 : $t_2=t_2+1$,go to Step 1 |
B. GA
遗传算法采用了生物遗传中优胜劣汰的思想,只要求问题是可计算的,忽略它是否可微、连续等。它从一组初始解开始,通过选择、交叉和变异进行优化,直到达成可接受的解决方案或收敛。交叉和突变的操作可以保持种群多样性,扩展搜索区域,故不容易陷入局部最优。
1) 染色体和适应度函数
染色体 expression(15)
使用real coded GA。一个个体由染色体定义,染色体是问题$P_0$的一个解决方案,某个种群的染色体和结构。为了减少要优化的变量的数量,将${A,B,P,F}$转化为$I$:
$$
I=[A^{} \space\space B^{}\space\space P\space\space F^{*}]^{\top}
$$
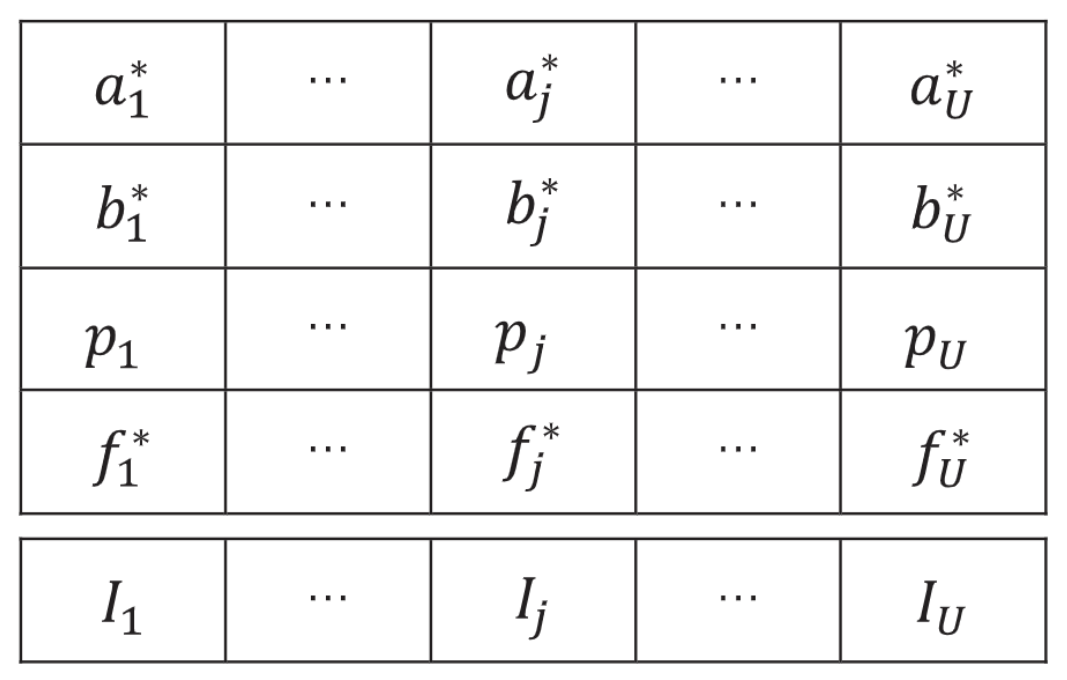
| 变量 | 意义 |
|---|---|
| $A^*={a^*_j,j\in N_B}$ | 计算卸载决策 |
| $a_j^*\in {-1}\cup N_B$ | UE-j选择的基站,-1代表没有选择 |
| $B^*={b^*_j,j\in u}$ | 可得到的信道 |
| $b_j^*\in 0\cup c_a$ | 分配给UE-j的信道 |
| $F^*={f_j^*,j\in u}$ | 可得到的计算资源 |
| $f_j^*\in [0,F]$ | 基站分配给UE-j的计算资源,F是基站总资源 |
| 图中的$I_j$ | 用户j的染色体 |
适应度函数
$$
Fitness=\sum_{j\in N_u}E_j(A,B,P,F)+Penalty
$$
$$
Penalty=\sum_{j\in N_u}\alpha_j[max(0,T_j(A,B,P,F)-t_j^{max})]
$$
| 变量 | 意义 | |
|---|---|---|
| $\alpha_i$ | 惩罚因素,不允许种群往不合适的方向发展,使种群收敛到可行的极端点。 | 仅约束$C_1$使用,因为在初始化和遗传操作中确保了其他的约束们 |
2)初始化和选择
初始化 expression(18)
算法1中的初始化是在此工作中随机生成的,但是在$P_0$的约束中(除了$C_1$)。初始种群的基因产生如下:
$$
a^{}_j(0)=randin({-1}\cup N_B)\
b^{}j(0)=randin({0}\cup c_a)\
p_j(0)=rand(p{max})\
f_j^{}(0)=rand(F_{a_j^{}(0)})
$$
$randin(Set)$是一个生成器函数,元素的输出是从随机选择器$Set.rand(x)$返回的,在$[0,X]$的随机数。对于$b_j^{}(0)$,有:
$$
\kappa = \begin{cases}
\emptyset,\space\space\space\space\space\space a_j^{}(0)=-1\
C_M,\space\space a_j^{}(0)=0\
C_S,\space\space\space a_j^{}(0)>0
\end{cases}
$$
选择
选择的方法上,采用了锦标赛,它是在选择父母时从K个人中选择最适合的一个。1. 计算成本较低,2. 选择好父母比只选择最好的父母更好。它保持多样性,并有机会培养更好的人, 3. 将其应用于最小化MINLP问题时无需修改。
3)交叉与突变
每次迭代中,应该用选择来维持父代,然后对父结点进行交叉和变异操作产生子结点。
交叉
随机选择两个父代,以交叉概率$p_c$交换对应的基因片段,从而产生两个后代。保持多样性。
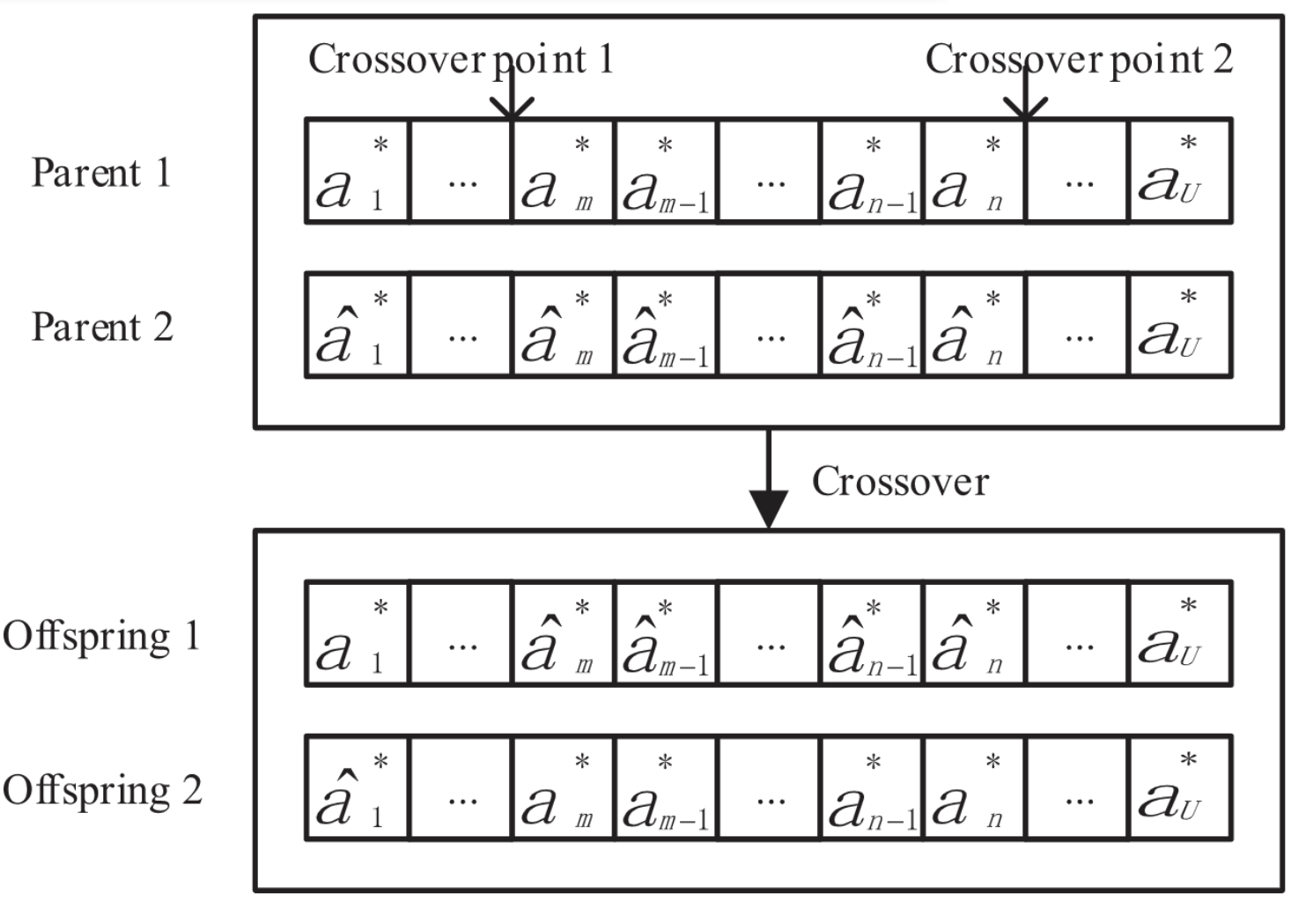
突变 expression(19)(20)
先选择一个个体,然后对染色体的每个元素,在表达式(15)定义后的变量范围内以突变概率$p_m$发生突变。
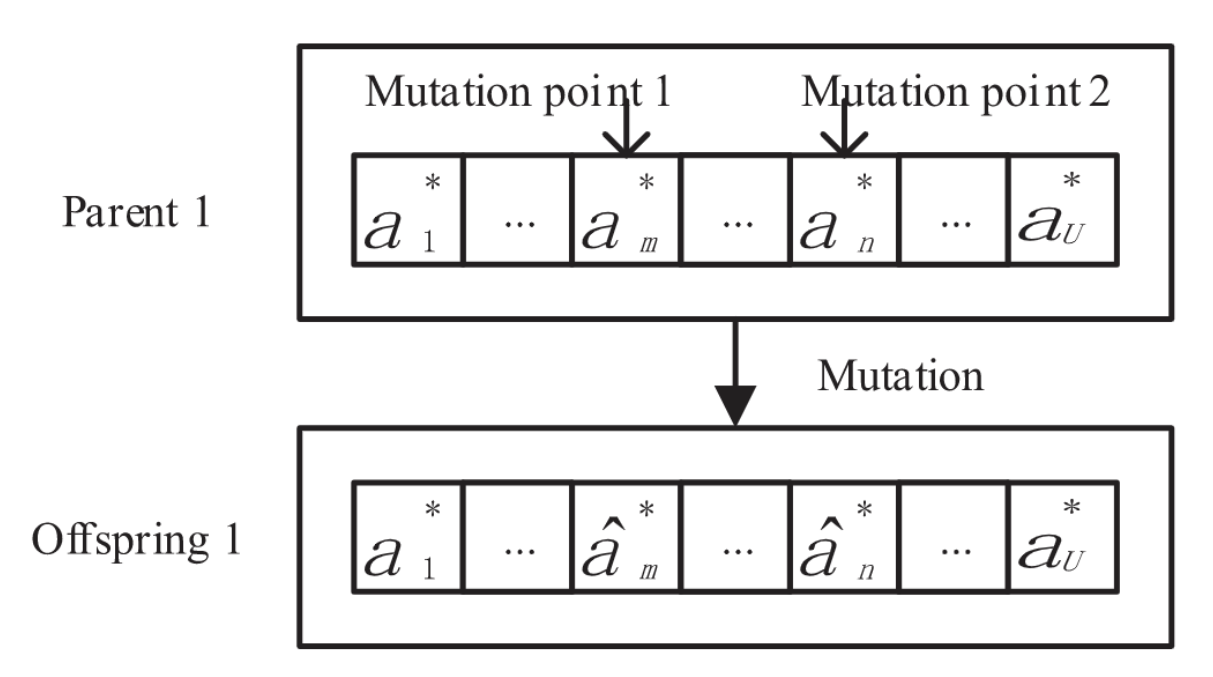
突变原理如下:
$$
\hat x ^{}_j=\begin{cases}
round(x_j^{}+\gamma_1(x_{max}-x_j^{})),
\space\space\gamma_2>0.5
\
round(x_j^{}-\gamma_1(x_j^{*}-x_{min})),
\space\space\gamma_2\le0.5
\
\end{cases}
$$
$$
\hat y ^{}_j=\begin{cases}
y_j^{}+\gamma_1(y_{max}-y_j^{}),
\space\space\gamma_2>0.5
\
y_j^{}-\gamma_1(y_j^{*}-y_{min}),
\space\space\gamma_2\le0.5
\
\end{cases}
$$
$x$ 代表前两行的整数变量,$y$代表后两行连续的整数变量。
$round(·)$是输出不超过$(·)$的整数。
$\gamma_1$,$\gamma_2$是两个(0,1)范围内的随机数
| 变量 | 意义 | |
|---|---|---|
| $x$ | 前两行的整数变量 | |
| $y$ | 后两行连续的整数变量 | |
| $round(·)$ | 输出不超过$(·)$的整数。 | |
| $\gamma_1$,$\gamma_2$ | 随机数$\gamma_1,\gamma_2\sim Uniform(0,1)$ | $\gamma_1$在局部搜索步骤调整中起作用,越大代表突变的幅度越大;$\gamma_2$控制着搜索方向,大于0.5时,向最大方向变化,反之。 |
| 在边界处不可行个体可以在一小步内成为可行,为了增加种群的多样性,算法2保留了一些不可行个体。 |
C. PSO exp(21)
粒子有速度、位置(基于社会信息共享)。粒子的位置表示所提问题的解,而速度表示解的演化过程。与GA相似,粒子的位置用$X=I$表示expression(15),粒子的速度:
$$
V=[V_1\space\space\space\space V_2\space\space\space\space V_3\space\space\space\space V_4]^{\top}
$$
粒子的速度 expression(22)
$$
V_{r,d}^{t+1}=wV_{r,d}^t+r_1c_1(pbest_{r,d}-X_{r,d}^{t})+r_2c_2(gbest_{r,d}-X_{r,d}^t)
$$
粒子的位置 expression(23)
$$
X_{r,d}^{t+1}=\begin{cases} \begin{aligned}
round(X_{r,d}^t+V_{r,d}^{t+1}),\space\space r=1,2\
X_{r,d}^t+V_{r,d}^{t+1}\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space\space r=3,4\
\end{aligned}\end{cases}
$$
$w$是惯性权值,$c_1$,$c_2$是瞬间加速度,$r_1$,$r_2$增加搜索随机性,在$[0,1]$之间。速度和位置不会超出expression(15)的约束。
D. 计算复杂性
初始化、适合度计算、选择、交叉、突变操作。每个->总体
初始化
| 内容 | 复杂度 |
|---|---|
| 初始化种群,生成基本的UEs和SBSs的信息,比如位置、计算卸载任务、计算资源 | $O(U+N)$ |
| 计算终端本地能耗和最大时延 | $O(U)$ |
| 生出初始化$K$个个体的复杂度 | $O(K\times U\times 4)$ |
初始化的总复杂度为
$$
O(U+N)+O(U)+O(K\times U\times 4)\approx O(K\times U+N), N<U
$$
GA 选择、交叉、突变
| 内容 | 复杂度 |
|---|---|
| 选择操作 | $O(K\times N_t),N_t$是一次锦标赛中的个体数量。 |
| 交叉操作 | $O(K\times 4)\approx O(K)$ |
| 突变操作 | $O(K\times U\times 4)\approx O(K\times U)$ |
| 基因操作总复杂度 | $O(T_1\times K\times N_t)+O(T_1\times K)+O(T_1\times K\times U)\approx O(T_1\times K\times U)$,满足$U>N_t>1$ |
| 评估个体 | $O(U^2)$ |
| 评估全部 | $O(T_1\times K \times U^2)$ |
GA 总复杂度为:
$$
O(T_1\times K\times U)+O(T_1\times K \times U^2)\approx O(T_1\times K \times U^2)
$$
PSO
| 内容 | 意义 |
|---|---|
| 评估 | $O(T_1\times K \times U^2)$ |
| 位置和速度更新 | $O(K\times U\times 4)\approx O(K\times U)$ |
PSO总复杂度:
$$
O(T_1\times K \times U^2)+O(K\times U)\approx O(T_2\times K\times U^2)
$$
总复杂度
$$
O(K\times U+N)+O(T\times T_1\times K\times U^2)+O(T\times T_2\times K\times U^2)\approx O(T\times T_1\times K\times U^2)
$$
$set \space \space T_1>T_2$
E. 收敛性分析
针对HGPCA,给出一些引理。
Lemma 1
HGPCA具有全局收敛性,当他满足:
1)下层GA在评估流程中总是包含最优解决方案;
2)惯性权值$w$、上层PSO的加速度常数$c_1,c_2$满足以下约束:
$$
\sqrt{2(1+w-\beta)^2-4w}<2
$$
且$\beta=\beta_1+\beta_2,\beta_1=c_1r_1,\beta_2=c_2r_2$
证明
虽然经典的GA是无法全局收敛到最优处的,但是GA的一个变体确是可做到的,那就是无论在选择前还是选择后,最佳个体总是存在于种群之中。在算法2中的第四步,总有用最优个体$I_{best}$代替最糟糕的个体。故底层GA是可收敛的。
对于PSO,已有证明它收敛于:
$$
X\to \frac
{\beta_1p_{best}+\beta_2g_{best}}
{\beta}
$$
假设全局最优为$g_{best}^{}$,当上层粒子群达到全局最优时,下层GA也达到全局最优点$g_{best}^$,故:
$$
X\to \frac
{\beta_1p_{best}+\beta_2g_{best}}
{\beta}
=
\frac
{(\beta_1+\beta_2)g_{best}}
{\beta}
=g_{best}^*
$$
仿真结果与讨论
A. 仿真设置
| 属性 | 值 |
|---|---|
| area | $1000\times 1000 m^2$ |
| maximum latency | 90% of the local latency |
| 算法 | 全称 | 解释 |
|---|---|---|
| GACA | genetic algorithm based | 遗传算法 |
| PSOCA | particle swarm optimizatio | 粒子群算法 |
| RCA | random | 随机算法,用户随机作出任务卸载决策、选择传输功率,SBS随机分配信道和计算资源 |
| LCA | local | 本地计算,用户选择在终端计算 |
| energy consumption | 能耗,指终端完成任务的总能耗 |
比较
| 算法 | 全称 | 解释 |
|---|---|---|
| JOIS | Joint Computation Offloading and Interference Management Scheme | 联合计算卸载和干扰管理方案,迭代优化变量 |
| VBFS | the optimal solution obtained by the verified Brute ForceSearching Algorithm | 暴力搜索的最优解。首先离散化连续变量,在一个相对小范围内搜索,使用HGPCA的解决方案来提高搜索效率 |
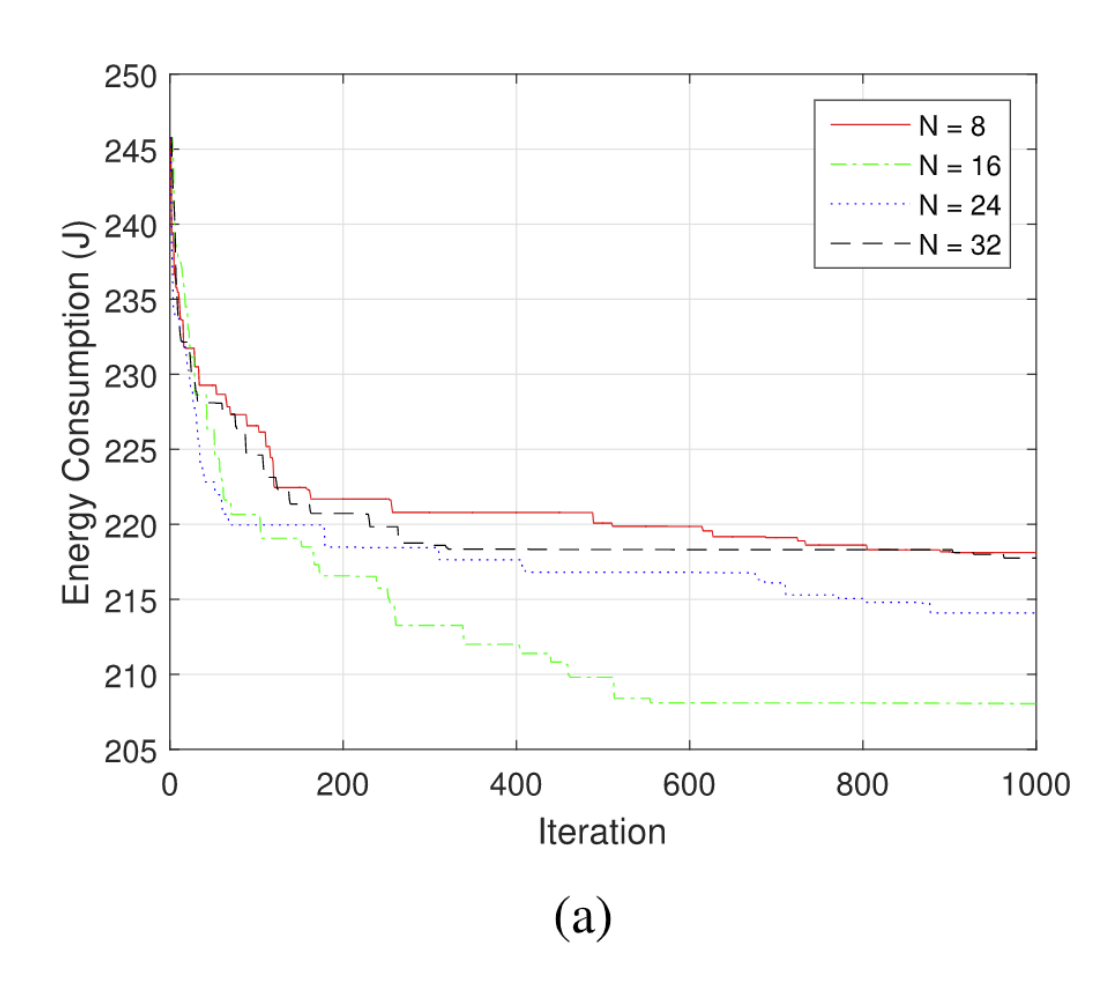
B. 收敛性分析
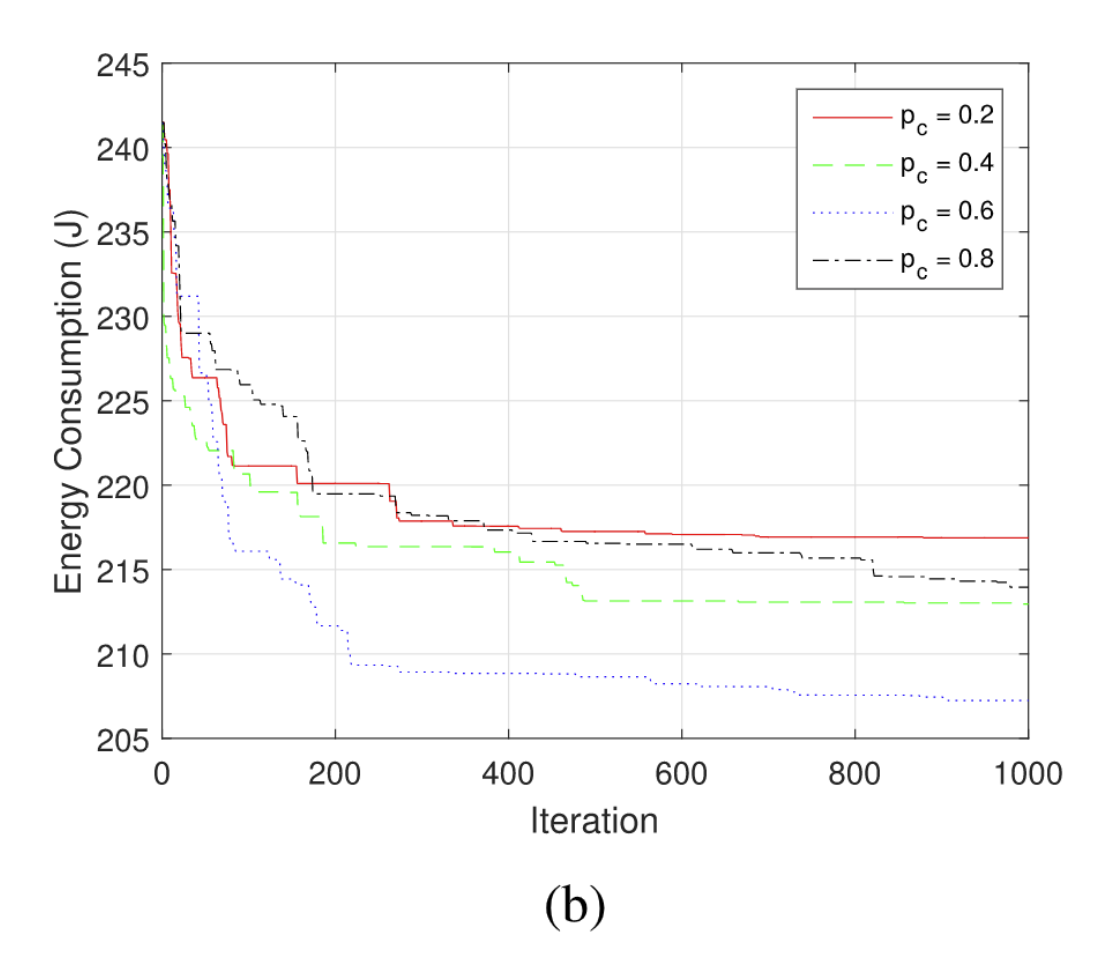
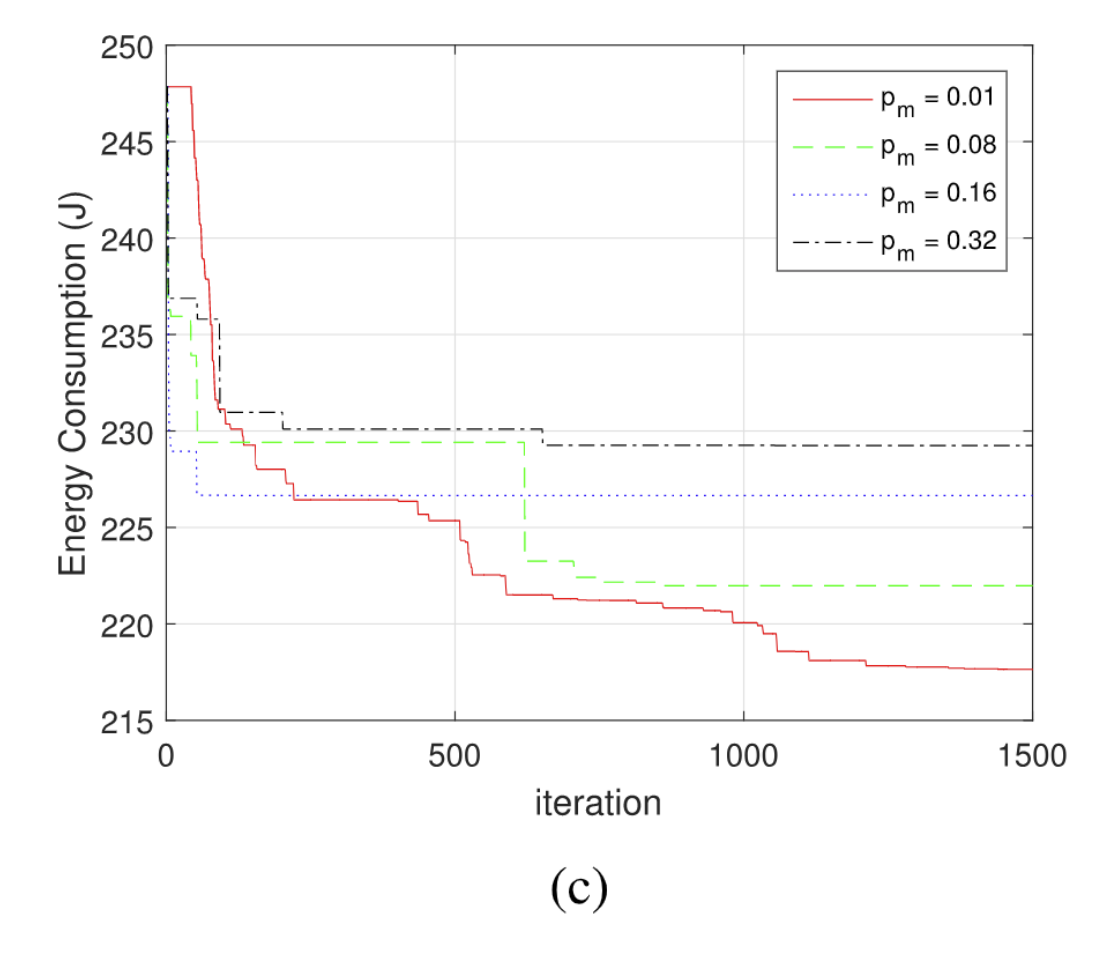
在遗传算法中,有三个重要的参数:不同的种群大小K、不同的$p_c$交叉概率,不同的$p_m$突变概率。
| $K$ | $p_c$ | $p_m$ |
|---|---|---|
 |
 |
 |
| $K=16$ | $p_c=0.6$ | $p_m=0.01$ |
| 当k很小的时候,无法保证种族多样性;当k很大的时候,一个小的变异可能无法包含最优解,因此需要更多迭代来收敛 | 当交叉概率很小的时候,对种群多样性的贡献很小,当交叉概率很大时,可能导致解的状态变差。 | 突变是很随机的,它不参考任何已知的信息,设计的本意是增加种群的多样性,而突变概率过大的时候可能会违背这个本意。 |
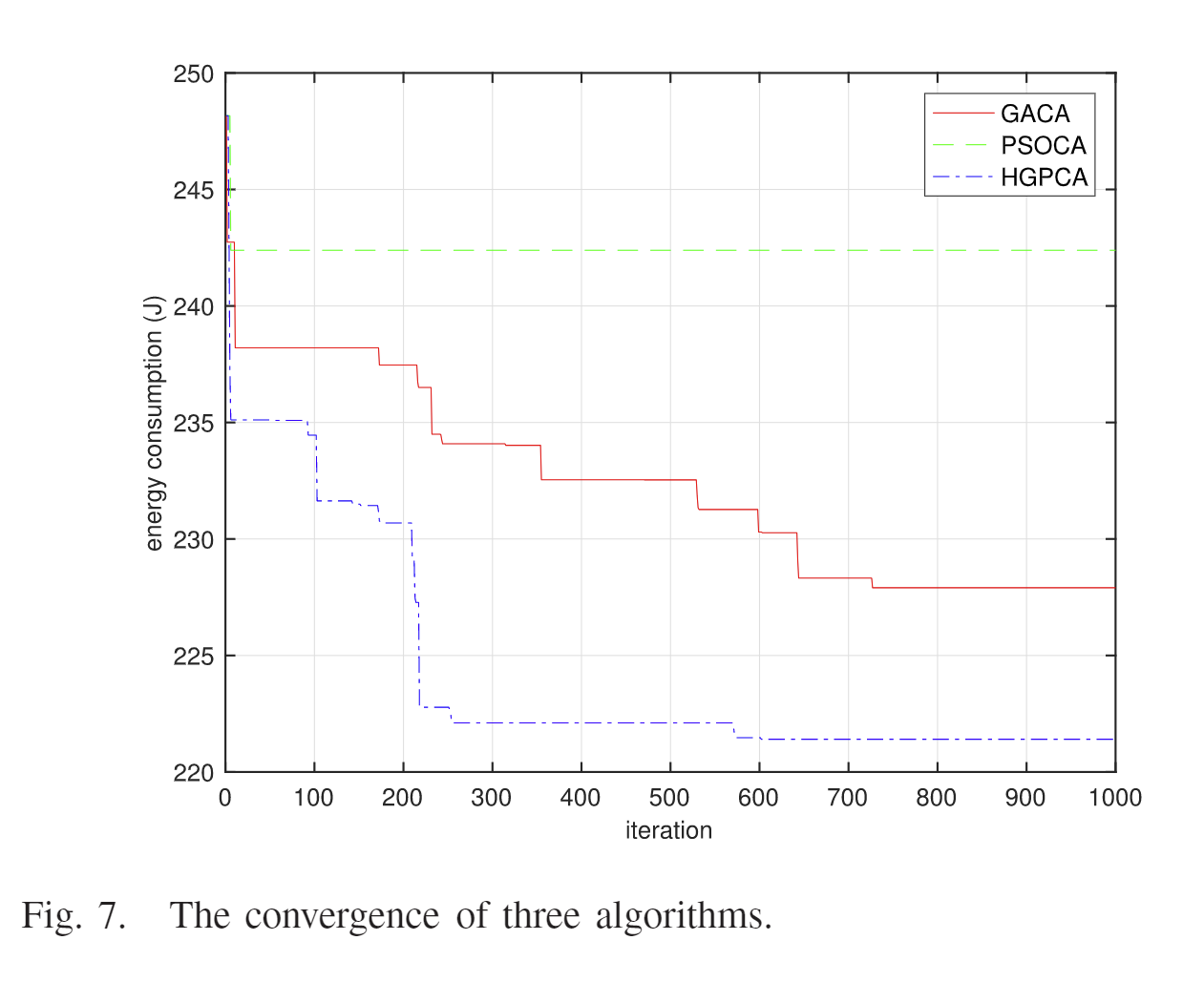
在上述参数下,跟GA与PSO算法对比,可以看到,PSO算法明显收敛最快,HGPCA次之,最后是GA;其次,HGPCA有着最低的能耗,PSO最高,这是因为HGPCA结合了两者的优点——GA更适合全局搜索、PSO更适合局部精确搜索。由于PSO收敛最快,因此它在传统的GA基础上,使算法的收敛速度提高。
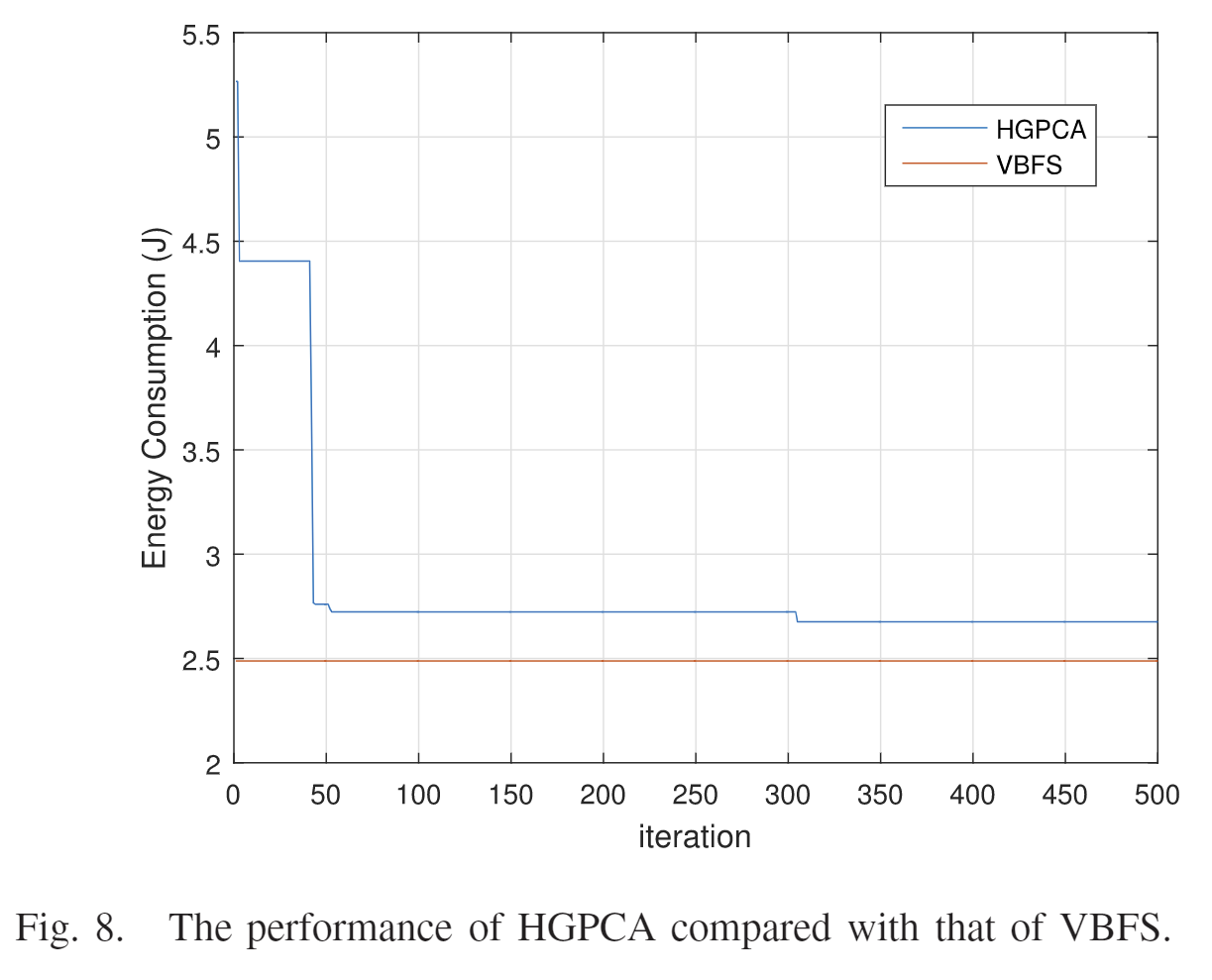
和暴力搜索相比,(4个SBS,4UE,随机分布在MBS,每个SBS有一个信道,2.4GHz)随着迭代,能耗减少,但迭代次数更加大时,性能优化不明显。
C. 性能分析
信道和计算资源不同
首先分析SBS不同资源量(信道和计算资源)对此算法的影响。然后,在各种参数下,与前面提到的其他基线算法进行比较后,可以验证所提出的算法。
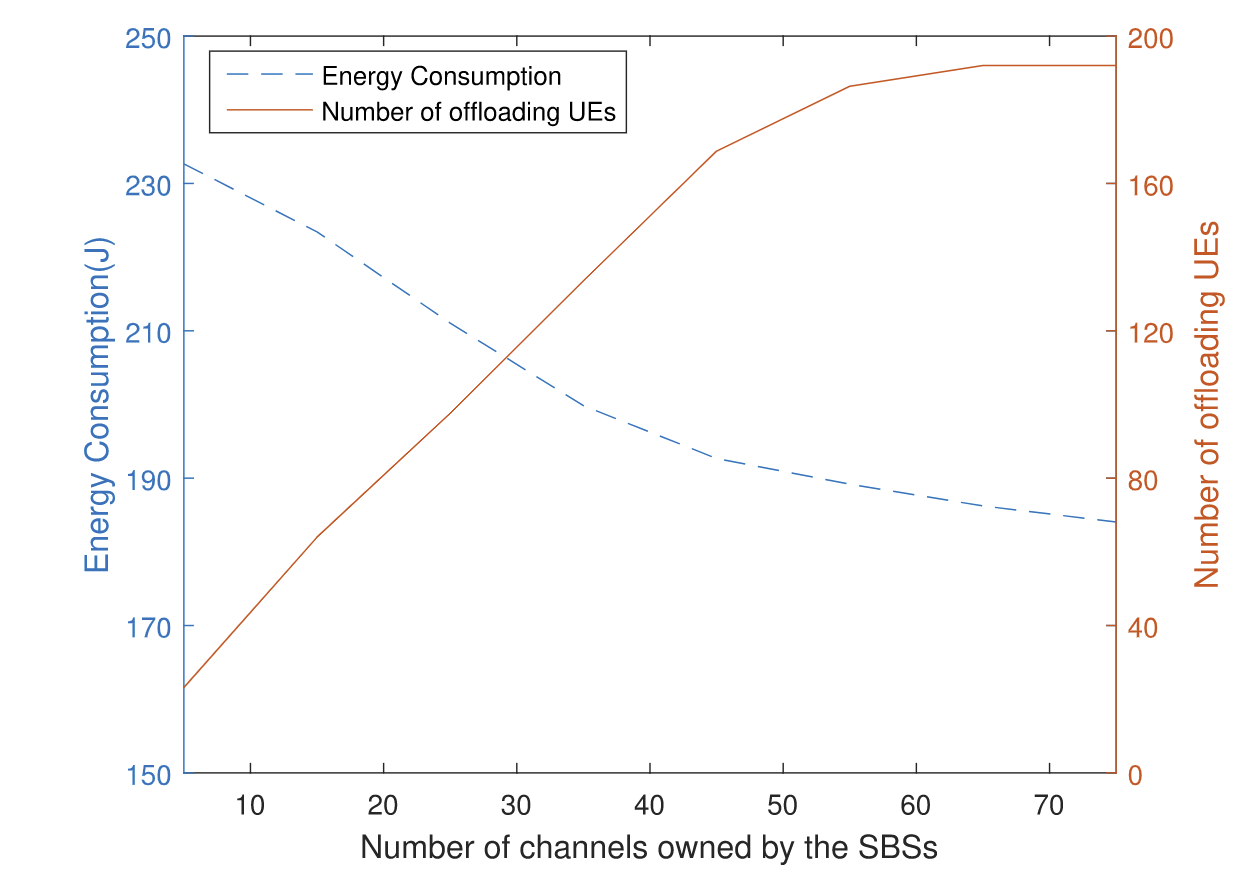
| SBS拥有的信道数量与能耗、卸载方案的关系 | SBS的计算资源与能耗、卸载的关系 |
|---|---|
 |
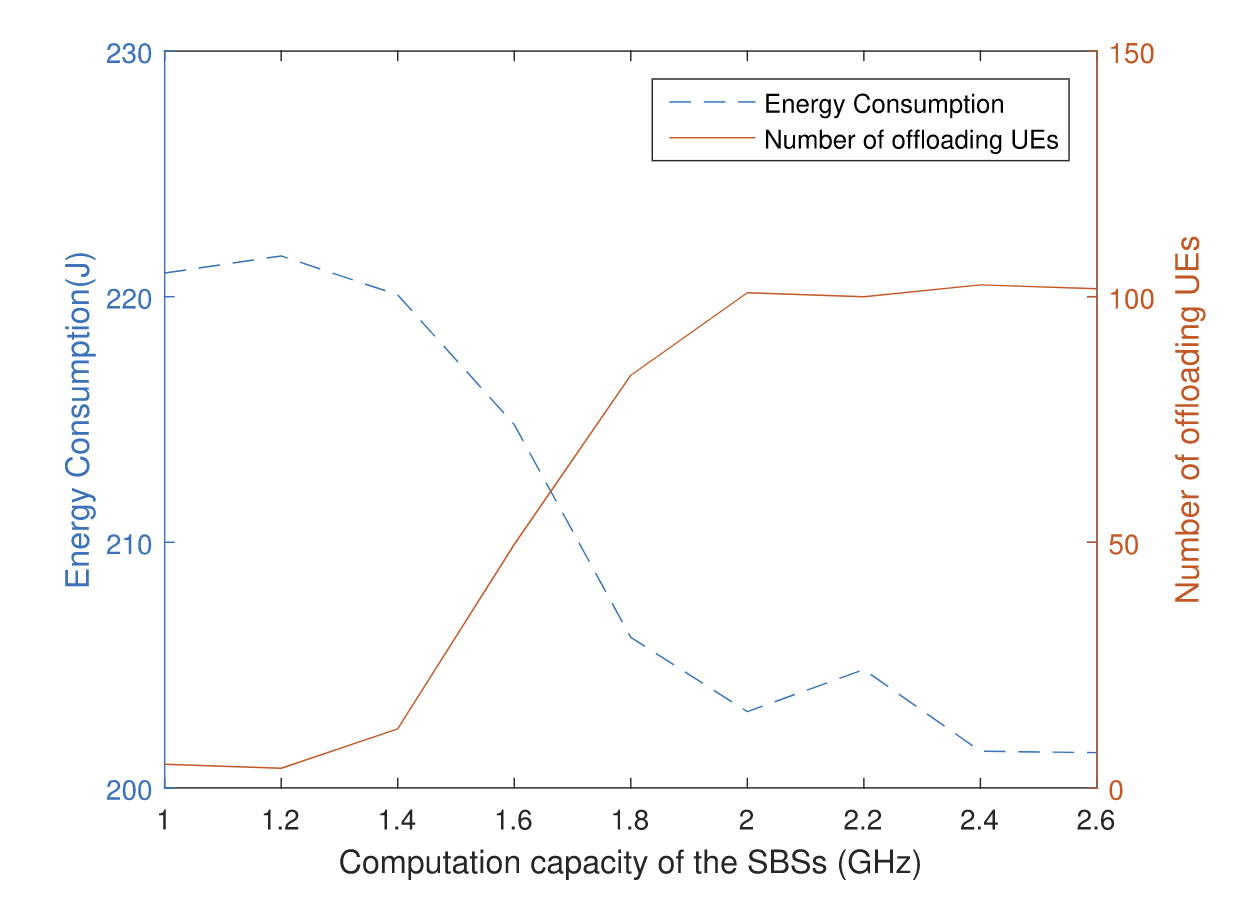 |
| (假设有足够的计算资源)不难看出,SBS的信道数量增加时,能耗会下降,UE中任务卸载数会上升。信道少的时候,UE之间的干扰就会很大,会导致时延,卸载少。 | SBS的计算资源与能耗、卸载的关系(信道30个)。资源增加时,能耗下降,卸载数增加。资源少,计算时间长,大多选择本地计算,能耗就高;资源多,计算时间就少,卸载的性价比就高。 |
| 当计算资源很多,传输时延就成了提高性能的绊脚石。无线资源和计算资源的匹配也很重要。 |
算法对比
GA/PSO/R/L
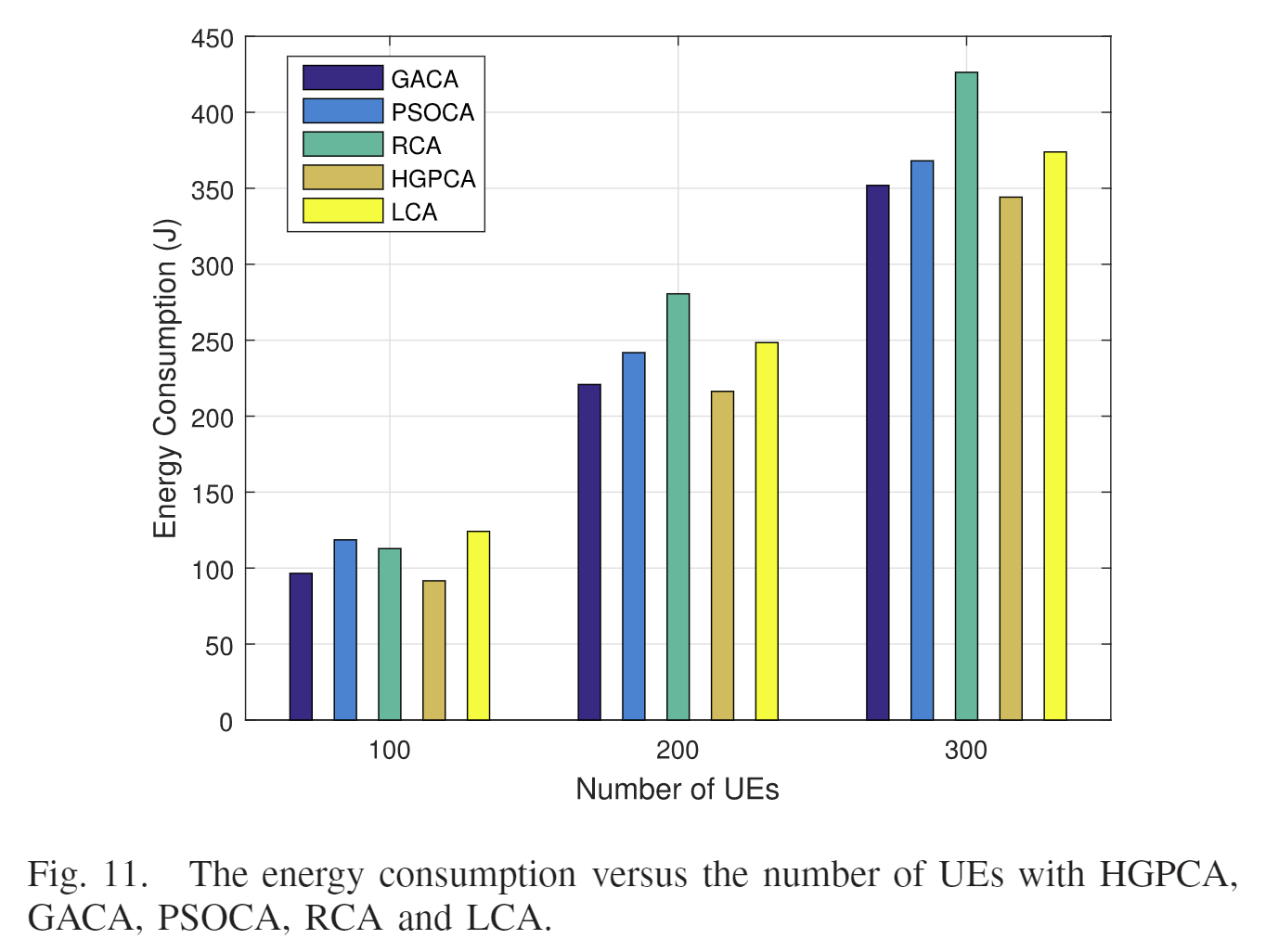
| UE: 100,200,300; SBS:49 | SBS: 36, 48, 64; UE: 200 |
|---|---|
 |
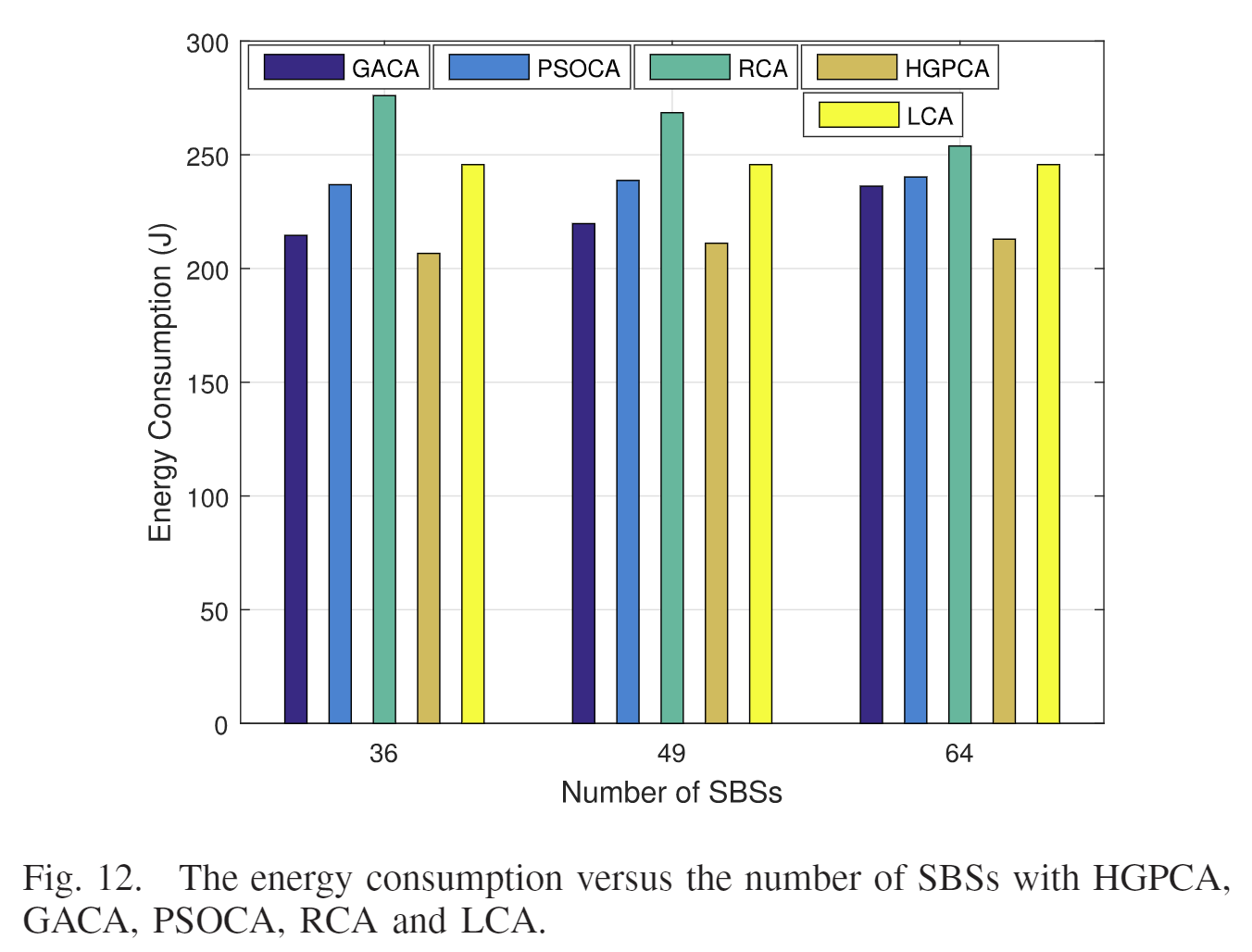 |
| 可以直观看出,HGPCA的能耗总是低于其他算法。 | 三种情况下,HGPCA能耗都是最低的。 |
| HGPCA的能耗随着UE增加而增加,因为任务数多了,UE之间的干扰也增加了。 | 系统包含更多的计算资源,同时干扰也增加了,因此既HGPCA与GA的能耗都增加。 |
| 由于UE不变,LCA的能耗不变;PSO不适合计算大范围的问题,总会陷入局部最优;RCA随机分配资源,所以性能不稳定。 |
| 算法 | 评价 |
|---|---|
| HGPCA | 能耗表现最低 |
| RCA | 由于是随机决策,会导致相邻终端之间的严重干扰,因此能耗可能会变得非常大。 |
| GACA | 对卸载、信道分配、功率控制、计算资源分配均有决策,控制卸载终端的数量和干扰,为UE节省能源。(全局最优 |
| PSOCA | 同上(局部搜索,收敛快,容易陷入局部最优 |
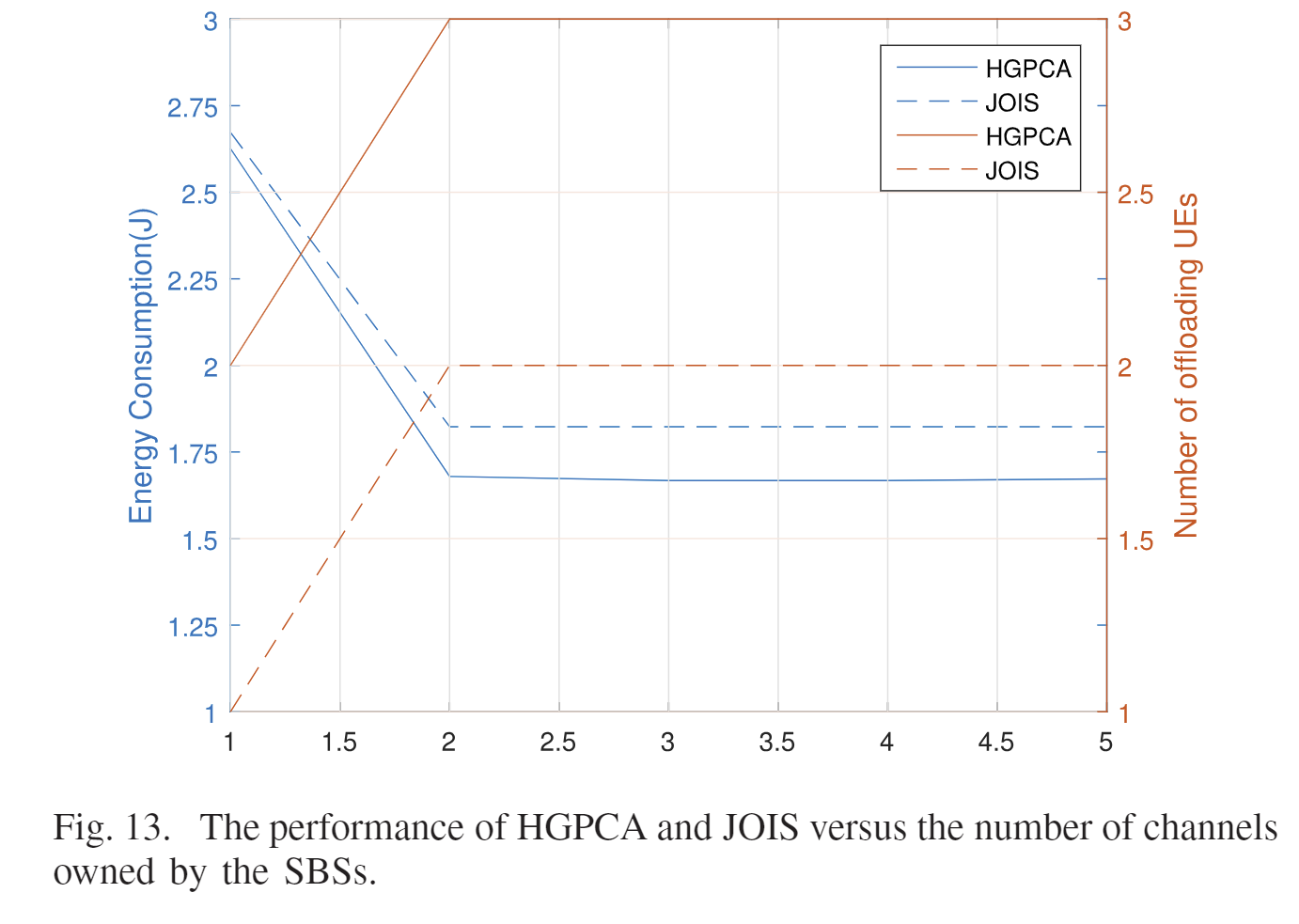
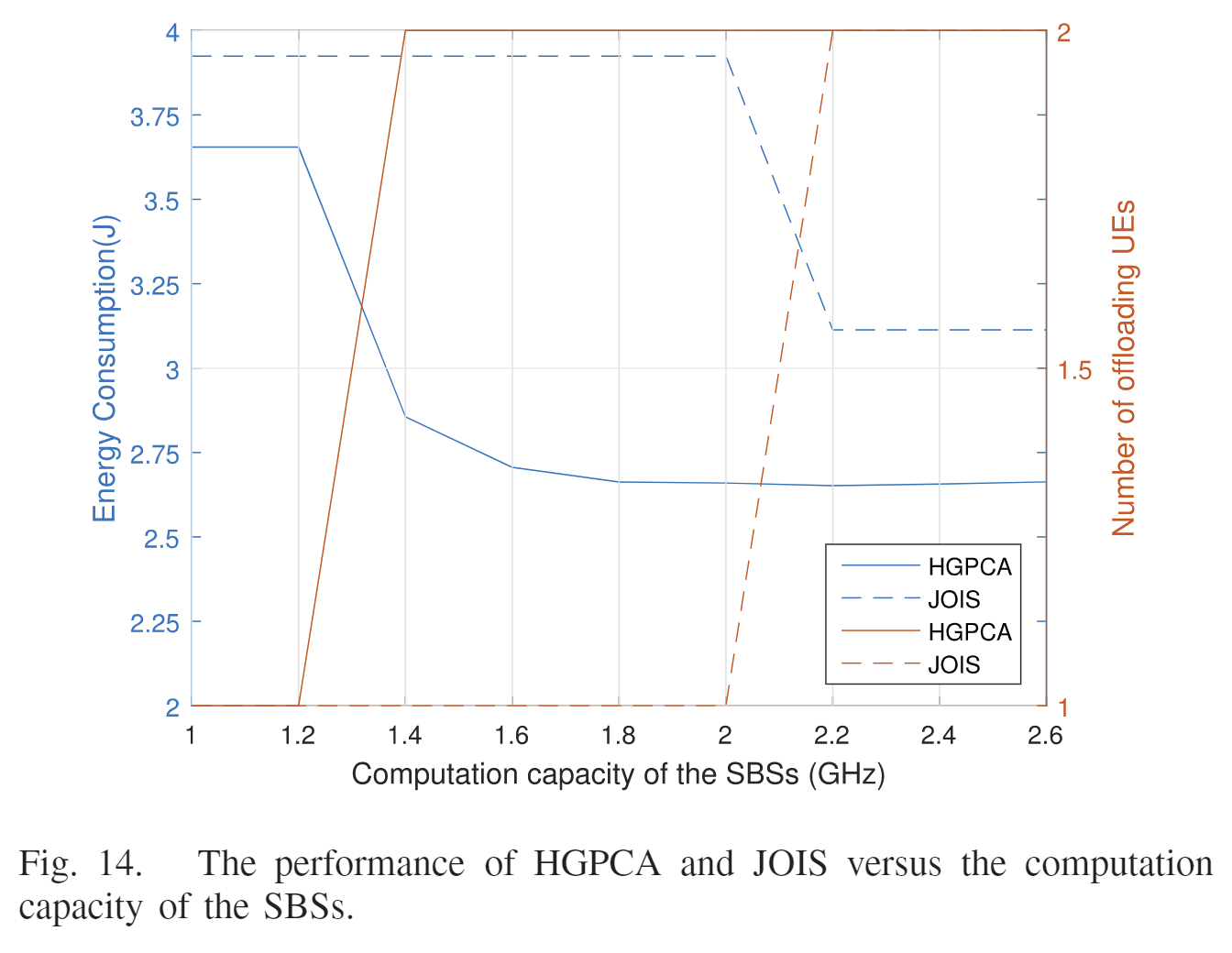
JOIS
| SBS信道数不同 | SBS计算能力不同 |
|---|---|
 |
 |
| 4SBS、4UE | |
| 随着信道数量上升,能耗都减少,但HGPCA的能耗一直都比JOIS低 | 随着SBS计算能力上升,能耗都降低,但是显然HGPCA的能耗一直低于JOIS |
| 随着信道数量上升,UE卸载任务数量都增加,但HGPCA的卸载数量高于JOIS | 随着SBS计算能力上升,任务卸载数量增加,但HGPCA的任务卸载分配要优于JOIS |
| 算法 | 评价 |
|---|---|
| HGPCA | |
| JOIS | 该算法只考虑能耗和根据本地时延分配给本地的计算资源,会导致资源利用率低。[24] |
