How many integers can you find
题意
一个n，一个长度为m的集合，集合里面有m个元素，问小于n的所有能被集合中任意元素整除的数字有多少。
n<2^31,m<=10
看！代码
1 |
|
容斥与鸽巢定理
容斥
公式
$$
|A_1∪A_2∪…∪A_n|=\sum_{i=1}^n|A_i|-\sum_{i=1}^n\sum_{j>i}|A_i∩A_j|+\sum_{i=1}^n\sum_{j>i}\sum_{k>j}|A_i∩A_j∩A_k|+…
$$
$$
+(-1)^{n-1}|A_1∩A_2∩…∩A_n|
$$
应用
错排问题
棋盘多项式与有禁区的排列
布棋问题
一个n*m棋盘上放k个棋子，其中任意两个棋子不能位于同一行或者同一列上。问种数。
布棋方案数 $R_k(C)$ : k个棋子依照上述规则放在棋盘C中的方案数
棋盘多项式： 棋盘C中放不限定数量的棋子,$R(C)=\sum_{k=0}^∞R_k(C)x^k$（有点母函数的味道），由于k<=C(格子数)，因此这个多项式也是有限的。
放置： $R_k(C)=R_{k-1}(C_x)+R_k(C_e)$
C表示这个棋盘，$C_x$表示放在棋盘C除去这个格子所在的行和列之后的棋盘，$C_e$表示棋盘C删去这个格子后的棋盘。
那么这个公式的意思就是，在棋盘C上放k个棋子的种数，等于（第k个棋子放在一个格子上，前k-1个数量的格子放在除了这个格子所在的行和列的地方），加上，（k个棋子放在除了这个格子的其他地方）。
棋盘多项式性质：
- $R(C)=xR(C_x)+R(C_e)$
- 若C由两个互不干扰的棋盘组成，有$R(C)=R(C_1)·R(C_2)$
有禁区的排列
排列数定理：
$$
n！-r_1(n-1)!+r_2(n-2)!-…±r_n
$$
$r_i$表示有$r_i$个棋子布置到禁区的方案数。（**仅适用n·n的棋盘**）
< 例题 > 有1,2,3,4号工人，A,B,C,D四个人物，1号不做B，2号不做B、C，3号不做C、D，4号不做D，问有多少种分配方式？
【解】先构造一个4*4的棋盘，然后画出这个棋盘的禁区，对于这个禁区计算它的棋盘多项式，得$R(C)=1+6x+10x^2+4x^3$，因此用容斥的思想，得到：
$$
4!- 6·(4-1)!+10·(4-2)!-4·(4-3)! +0(4-4)!= 4
$$
鸽巢定理
基本定理
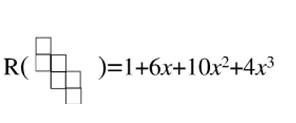
n+1只鸽子飞回n个鸽巢，至少有一个鸽笼含有不少于2只的格子。
数学描述：
m($1\le m$)个元素分成n个组，那么总有一个组至少含有元素个数$\lceil\frac{m}{n}\rceil$
小应用
对于正整数序列，$a_1，a_2，…，a_m$，至少存在整数k和l, $1\le k<l\le m$，使得$a_k+a_{k+1}+…+a_l$是m的倍数。
【证明】对每个元素$a_i$构造一个前缀和sum[i]，则有两种可能性：
(1) 若有一个sum[i]是m的倍数，则证毕；
(2) 若没有一个sum[i]为m的倍数，则令$r_h\equiv S_h mod\ m $ 。
其中，h=1,2,…,m，我们已知上面所有的项都非m的倍数，故余数r[i]的范围在[1,m-1]，共m个数，根据鸽巢定理，m个余数在[1,m-1]共m-1的范围内至少存在一对$r_h$,$r_k$，满足$r_k=r_h$,则sum[k]和sum[h]满足：
$$
S_k\equiv S_h mod \ m
$$
设h>k的话，得到
$$
S_h-S_k=(a_1+a_2+…+a_h)-(a_1+a_2+…+a_k)
=a_{k+1}+…+a_h\equiv 0\ mod \ m
$$
证毕。中国剩余定理
GCD?LCM!(莫比乌斯反演)
GCD?LCM!
题意
哈哈哈哈哈懵逼钨丝做的我一本满足，爽歪歪，推公式好塔马有趣儿
咳咳，题目是：
$$
F(n)=\sum_{i=1}^n\sum_{j=1}^n[lcm(i,j)+gcd(i,j)\ge n]
$$
$$
S(n)=\sum_{i=1}^nF(n)
$$
t组，每组给你一个n，求S(n)。
t<=1e5,n<=1e6
思路
$$
F(n)=\sum_{i=1}^n\sum_{j=1}^n[lcm(i,j)+gcd(i,j)\ge n]
$$
$$
=\sum_{i=1}^n\sum_{j=1}^n[lcm(i,j)+gcd(i,j)\ge n-1]-\sum_{i=1}^n\sum_{j=1}^n[lcm(i,j)+gcd(i,j)==n-1]
$$
由于对于后半部分来说，i，j=n时显然不符合，因此可直接降为n-1
$$
=\sum_{i=1}^n\sum_{j=1}^n[lcm(i,j)+gcd(i,j)\ge n-1]-\sum_{i=1}^{n-1}\sum_{j=1}^{n-1}[lcm(i,j)+gcd(i,j)==n-1]
$$将前半部分转化成F(n-1)，故修改i，j的上限，而i，j=n时一定满足要求，因此要补上2n-1
$$
=\sum_{i=1}^{n-1}\sum_{j=1}^{n-1}[lcm(i,j)+gcd(i,j)\ge n-1]+(2n-1)-\sum_{i=1}^{n-1}\sum_{j=1}^{n-1}[lcm(i,j)+gcd(i,j)==n-1]
$$
$$
=F(n-1)+(2n-1)-\sum_{i=1}^{n-1}\sum_{j=1}^{n-1}[lcm(i,j)+gcd(i,j)==n-1]
$$
令后半部分为T(n-1),则：
$$
F(n)=F(n-1)+(2n-1)-T(n-1)
$$
接下来分析T(n)
$$
T(n)=\sum_{i=1}^n\sum_{j=1}^n[lcm(i,j)+gcd(i,j)==n]
$$
令d=gcd(i,j)，又由于lcm(i,j)=ij*(gcd(i,j))，令i=id，j=jd
$$
=\sum_{d|n}\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum_{j=1}^{\lfloor\frac{n}{d}\rfloor}
[ijd+d==n][gcd(i,j)==1]
$$
$$
=\sum_{d|n}\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum_{j=1}^{\lfloor\frac{n}{d}\rfloor}
[j=\frac{\frac{n}{d}-1}{i}][gcd(i,j)==1]
$$
$$
=\sum_{d|n}\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}
[gcd(i,\frac{\frac{n}{d}-1}{i})==1]
$$
由于$\ i = \frac{n}{d}$ 时，条件显然不成立，因此修改i的上限
$$
=\sum_{d|n}\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor-1}
[gcd(i,\frac{\frac{n}{d}-1}{i})==1]
$$
令后半部分为$ G(\frac{n}{d}-1) $
$$
T(n)=\sum_{d|n}G(\frac{n}{d}-1)
$$
接下来分析G(n)
$$
G(n)=\sum_{i=1}^n[gcd(i,\frac{n}{i})==1]
$$
要满足后半部分，我们打表（或者根据思考（？？？））发现
$$
G(n)=2^k,k为n的质因子个数
$$
那么到这里，基本上要推的就都推完了，
差一个总和。
由于：
$$
F(n)=F(n-1)+(2n-1)-T(n-1)
$$
$$
=F(n-2)+(2(n-1)-1)-T(n-2)+(2n-1)-T(n-1)
$$
$$
=F(n-3)+(2(n-2)-1)-T(n-3)+(2(n-1)-1)-T(n-2)+(2n-1)-T(n-1)
$$
$$
……
$$
$$
=F(1)+\sum_{i=1}^n(2i-1)-\sum_{i=0}^{n-1}T(i)
$$
故：
$$
S(n)=\sum_{i=1}^n(F(1)+\sum_{j=1}^i(2j-1)-\sum_{j=0}^{i-1}T(j))
$$
$$
S(n)=nF(1)+\sum_{i=1}^ni^2-\sum_{i=1}^n\sum_{j=0}^{i-1}T(i)
$$
$$
=n+\frac{n(n+1)(2n+1)}{6}-\sum_{i=1}^n\sum_{j=0}^{i-1}T(i)
$$
我们一步一步来：
- 预处理，先筛出所有质数，然后是1~1e6的质因子个数，然后求得G(n)，再求得T(n)，然后对T(n)求一次前缀和得到每个sum[i]，再对每个sum[i]求前缀和ans[i]=sum[i-1]+ans[i-1]。
- 没有2了，对于每个输入的n直接用刚刚最后那个公式带进去算就好了：
$$
S(n)=n+\frac{n(n+1)(2n+1)}{6}-ans[n]
$$
哦，别忘了取模。
看！代码
1 |
|
带劲and和（连通块+&结论）
带劲的and和
题意
度度熊有一张n个点m条边的无向图，第i个点的点权为vi。
如果图上存在一条路径使得点i可以走到点j，则称i,j是带劲的，记f(i,j)=1；否则f(i,j)=0。显然有f(i,j)=f(j,i)。
度度熊想知道求出：
$\sum_{i=1}^{n−1}\sum_{j=i+1}^nf(i,j)×max(v_i,v_j)×(v_i&v_j)$
其中&是C++中的and位运算符，如1&3=1, 2&3=2。
请将答案对109+7取模后输出。
思路
先处理连通块。
这里我用的是并查集，也可以用tarjan，然后对于每个连通块里的元素，我们按照从小到大排序。
由于比如 9 8 7 这部分时，默认我们已经知道9是最大的元素，那么一定是9*(9&8+9&7),由于与运算是只有两位上的数字均为1时才能有贡献，那么也就是说，我们不需要对于每两个数字都计算&运算，而可以对每一个数字的二进制位进行处理，当第i位上为1时，count[i]++，只有count[i]上的数>=2时，才算对于这个有了贡献，并且我们是用同一的9去进行与运算，在count位>=2时，也只有满足当9上的第i位也为1时才算数。
因此从小到达排序之后，从第一个元素开始，在它前面的元素一定比它小，因此我们只要对于这个元素上为1的位进行查询，看它的count是否大于等于2，然后确定是否产生贡献，ans+了后再把当前元素的这一位的count[i]++即可。
看！代码
1 |
|
Mophues(莫比乌斯反演)
Mophues
题意
若a的质因子个数<=P，则称a为p的一个lucky number。
给你n，m，P，求在n，m范围内的i，j，gcd(i,j)是P的lucky number，这样的i，j有几对？
n，m，P<=5e5。多组不超过5000组。
思路
题意就是让我们求：
$$
\sum_{i=1}^n\sum_{j=1}^mf(gcd(i,j)),其中f(x)表示x的质因子个数比p小
$$
反演过程就不具体写了，我们可以轻松得到结果：
$$
\sum_{t=1}^{min(n,m)}\lfloor\frac{n}{t}\rfloor\lfloor\frac{m}{t}\rfloor\sum_{d|t}f(d)μ(\frac{t}{d})
$$
经过计算我们发现，5e5内的数字最大的质因数个数为18，那么对于大于18的p我们就可以降为18。
首先对5e5内的数预处理出它们的质因子个数。
然后枚举d，用sum[i][j]表示当t=i时，质因子个数为j的数的μ之和。
再对sum[i][j]求t=i时质因子个数小于等于j的μ之和。
然后对每一个t的sum求一个前缀和。
就可以分块做了。
注意ans和sum还是要开longlong。
看！代码
1 |
|
CA Loves GCD(DP)
CA Loves GCD
题意
给你n个数，从里面任取几个（至少1个），计算它们的gcd，问你所有可能的取法的gcd之和。
对结果模1e8+7（注意是8）
n<=1000
思路
dp[i][j]表示取前i个数时gcd为j的种数。
取第i个时：dp[i][gcd(a[i],j)] += dp[i-1][j] ；
不取第i个时：dp[i][j] += dp[i-1][j]；
对1000内的任意两个数的gcd作预处理，i从0开始。
看！代码
1 |
|
Hillan and the girl(莫比乌斯反演)
Hillan and the girl
题意
对于1<=n,m<=1e7，T<=1e4，求：
$$
\sum_{i=1}^{n}\sum_{j=1}^{m}f(gcd(i,j)),其中f(x)=1，当且仅当x为平方数
$$
思路
来，让我们来反演一波：
$$
\sum_{d=1}^{mim(n,m)}f(d)\sum_{i=1}^n\sum_{j=1}^m[gcd(i,j)==d]
$$
$$
\sum_{d=1}^{min(n,m)}f(d)\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum_{j=1}^{\lfloor\frac{m}{d}\rfloor}[gcd(i,j)==1]
$$
$$
\sum_{d=1}^{min(n,m)}f(d)\sum_{i=1}^{\lfloor\frac{n}{d}\rfloor}\sum_{j=1}^{\lfloor\frac{m}{d}\rfloor}\sum_{t|gcd(i,j)}μ(t)
$$
$$
\sum_{d=1}^{min(n,m)}f(d)\sum_{i=1}^{\lfloor\frac{n}{dt}\rfloor}\sum_{j=1}^{\lfloor\frac{m}{dt}\rfloor}\sum_{t=1}^{min(\lfloor\frac{n}{d}\rfloor,\lfloor\frac{m}{d}\rfloor)}μ(t)
$$
$$
\sum_{d=1}^{min(n,m)}f(d)\sum_{t=1}^{min(\lfloor\frac{n}{d}\rfloor,\lfloor\frac{m}{d}\rfloor)}μ(t){\lfloor\frac{n}{dt}\rfloor}{\lfloor\frac{m}{dt}\rfloor}
$$
令dt=T，则：
$$
\sum_{T=1}^{min(n,m)}{\lfloor\frac{n}{T}\rfloor}{\lfloor\frac{m}{T}\rfloor\sum_{d|T}f(d)}μ(\frac{T}{d})
$$
由于$d=x^2$
$$
\sum_{T=1}^{min(n,m)}{\lfloor\frac{n}{T}\rfloor}{\lfloor\frac{m}{T}\rfloor\sum_{x=1}^{min(\sqrt{n},\sqrt{m})}\sum_{x^2|T}}μ(\frac{T}{x^2})
$$
对于T的前半部分，我们可以用分块，复杂度为$\sqrt{n}$，对于后半部分，就可以预处理出来。
枚举x，以及每一个$x^2$的倍数$k·x^2$，处理出每一个T的对应的值，然后再求前缀和。
预处理部分的复杂度为O(n)，求的时候的复杂度为$O(T\sqrt{n})$。
看！代码
1 |
|
はなび
我发现日本的电影或者是电视剧，总是生活的样子，不会把片子的色调调的明亮而饱和，不会把每个人脸上的斑点、皱纹、坑坑洼洼悄悄隐藏，而让坐在荧幕前面的我们只看到光滑的皮肤和胶原蛋白。
是走在大街上能看到的，二十多岁小姑娘，三四十岁的工厂的妇女，建筑工地上的工人，和蔼的老婆婆，还有那怯生生的孩子。
是贫穷的屋子里面拥挤的住着五口人，角角落落塞得满满当当。
是即使辛苦艰难，其中偷偷夹带着的小幸福。
尽管我从一开始就知道，他们并不是”一家人“。
尽管我想，要是一直在一起就好啦。
柴田在废弃的车子中找到不高兴的祥太，告诉他由理是他”妹妹“，你要叫我”爸爸“（祥太一直叫不出口），瘸着腿在路上和祥太玩闹；
信代和由理泡着澡，由理看见信代手臂上的伤疤，和妈妈用熨斗烫伤自己的伤疤一样，心疼的不停轻轻抚摸着信代受伤的地方，信代说谢谢你，已经一点都不疼啦；
洗完澡把由理来时的旧衣服烧了，信代紧紧的抱着由理，悲伤的好像要把由理揉进自己的怀抱里。对由理说才不是由理的错，如果有人说爱你才打你，那才不是真的，如果爱你的话，就会像我这样，这样抱着你；
大家一起看烟花，可是只听得见烟花的声音，却看不到烟花；
小卖铺的爷爷早就知道祥太总是把东西偷偷顺走，只是当看到由理也学着祥太的样子偷窃，他学着他们偷东西前的手势，告诉祥太，以后不要叫你妹妹这样了，然后送了他们两个果冻，祥太问要继续偷吗，柴田说超市里放着的东西不属于任何人，除非倒闭了；
大家一起去海边的时候，奶奶对信代说”你真漂亮，脸蛋“，后来信代也跑去和大家玩，然后奶奶一个人坐在沙滩上面，把沙子洒在自己长满老年斑的小腿上，看着这一瞬间的”家人们“，无声的说”谢谢你们“；
信代为了保住由理，丢了工作，和柴田在家里吃着面，她走去厨房，雷雨前的最后一丝阳光透过窗户落进来，信代穿着透明凉快的衣服，汗水浸湿了头发，浸湿了脸庞，浸湿了胳膊，柴田看呆了，信代亲了柴田，然后终于打雷了，大雨来了，屋子里都是热乎乎，热乎乎的味道。
但是总会被打破的。
奶奶在从海边回来后的某天安静的离开了，柴田想打救护车，信代却说，你敢叫救护车吗。殡仪馆火化这么贵。我们哪有钱。由理也想和奶奶一直在一起吧。那我们就一直陪着奶奶吧。于是在自家挖坑把奶奶埋葬了。
亚纪一直伤心。柴田对祥太说，我们一直是五个人，从来没有奶奶。
信代取了奶奶的银行卡，找到了奶奶藏起来的钱，和柴田开心的大笑。
柴田带着祥太砸车偷包，祥太开始不愿意这样做了。
便利店的爷爷也去世了。祥太带着由理去超市，叫由理在外面等着。由理却跑进来想和哥哥一起偷。祥太看见还这么小的妹妹，笨拙的学着自己，把一包零食塞进自己的衣服里，塑料包装发出响声。他看了一会，在店员面前抢了一带柚子，转身就跑。然后被店员追上，从桥上跳下去。他终于认识到，这样的生活，已经不能再继续下去了。他是故意的呀。
大家被发现了。想要抛下在医院的祥太逃跑，还是没有成功。
”你们并不是一家人啊。“
”奶奶的尸体呢？抛尸可是犯罪啊。“
”为什么要诱拐孩子呢？“
”柴田你啊，祥太是你的本名把？“
”叫孩子偷窃，内心不会愧疚吗？“
”听说那两个人是杀了前夫呢。“
”奶奶一直有从你父母那里拿钱哦。“
”是因为自己生不出孩子，才嫉妒别人，才会诱拐孩子的吧。”
”树理（由理）的画颜色真好看呀，终于能回家了呢。“
“祥太你呀，以后就能去学校上学啦。”
”他们是怎么称呼你的呢？妈妈？母亲？“
……
解散了，这样的羁绊。
道德的制高点，大概看不见渺小的尘埃。
总会有些疑惑，比如为什么信代失业，柴田却理所当然的说你可以重拾老本行；奶奶死的时候，信代和柴田没有一点难过的样子，没过多久就拿了奶奶的养老金窃喜；为什么明明从前给了祥太这般的慈爱和体贴，却还是决定抛弃他，偷偷溜走。
柴田追赶着公交车，大声呼喊祥太的名字，车上的祥太却只是向前看，无动于衷。但是末了却转过头，轻声的说了一声”爸爸“。祥太对柴田的爱的认可，是真的，希望自己能够追寻另一种人生，也是真的。
只是柴田永远听不见这句”爸爸“，就像奶奶在海边说的”谢谢“，就像亚纪一直在从父母那里拿钱的时候，以为奶奶并不是喜欢她，才收留她的，是因为钱，她永远不知道奶奶一分钱没花。我想起她问柴田，维系两个人之间的东西到底是什么？是钱啊。
是利益吗？让这个家庭组合在一起？
我想是的，私利是让他们走在一起的原因，是让他们一起生活的原因，是让他们选择彼此的原因。这并不影响我对你的关心。只是这样的选择，比起自己原本的人生，好了太多了。
私欲是真的，背叛是真的，爱也是真的。
无法讨论人性，因为无情之中又饱含着万千真情。
世界并不是完美的乌托邦，也并非地狱的修罗场。
每个人都有每个人的活法。
也许我根本没有看懂这部电影，很多人都说看不懂。只是很喜欢这样的电影。我想起自己看《人间失格》电影的时候，开头，一条弹幕：
”你不需要看懂这部电影，你只要知道，有人这样活着就好了。“
他呈现的不是道德的是非，而是道德的困境。
他帮你撕掉人们身上的标签，让你看见那一个一个人。那些和你一样，有血有肉，有夜里开着灯等他们回家的亲人。
他尽力展现生活的复杂，让你看到算计，也看到算计背后的温情，让你了解，体谅，让你珍惜”有点肮脏的世界，忽然变得美好了起来的瞬间。“
整数划分(裸五边形定理)
不可重复的数字划分（基础dp）
1 |
|
1259 整数划分 V2
1 | //可重复的划分，五边形定理 |
Little Bishops（棋盘禁区排列）
[Little Bishops](https://vjudge.net/problem/UVA-861)
题意
在国际棋盘中，象的走法是斜对角线，也就是说两个象不能容于一条斜对角线。国际象棋有黑白两色格子相交组成。给你n*n的棋盘和k个象，问你在满足任意两个象互不相斥的情况下，摆放的最大种数？
思路
利用棋盘禁区排列这一思想。
首先我们可以看到，在棋盘中，黑色的格子和白色的格子上的象绝对不会相斥，所以我们可以根据$R_k(C)=R_i(C_1)*R_{k-i}(C-C_1)$得，Ans就是在黑色棋盘上放i个象的种类乘以在白色棋盘上放k-i个象的种数。
为了将黑白棋盘分开，比如要建立一个方便的白色棋盘，斜着看显然不舒服，那么我们就：
先把黑色格子删去，然后我们斜+45度看这个棋盘，把一斜看做一行，一斜中的格子数就是一行的格子数，同样的，斜-45度就是列中的格子数。又因为每行互换位置并不影响最终结果，因此我们可以把原本对称的棋盘行，进行格数从小到大排序，得到最终的棋盘。
注意，由于黑白棋盘不一样，对于一个n*n的棋盘来说，斜+45度看一共有2n-1个斜行，因此我们这里让白色棋盘占n行，黑色占n-1行，然后用另外的一个数组来存每行中有多少格子（列），基本的构造棋盘就完成了。
对于构造出来的棋盘（如白色），分析一下：
设mp[i][j]表示前i行放j个棋子的种数。那么有
$$
mp[i][j]=mp[i-1][j]+mp[i-1][j-1]·(c[i]-(j-1))
$$
相当于=前i-1行放了j个棋子，这一行不放的种数，加上前i-1行放了j-1个棋子乘以这一行只能在（格子数-已经被j-1个象占了的格子数量）个格子。
对两个棋盘都进行这样的操作即可。
最后的答案就是$\sum_{i=0}^{k}R_i(C_{white})·R_{k-i}(C_{black})$
看！代码
1 |
|
缺失模块。
1、请确保node版本大于6.2
2、在博客根目录（注意不是yilia根目录）执行以下命令：
npm i hexo-generator-json-content --save
3、在根目录_config.yml里添加配置：
jsonContent:
meta: false
pages: false
posts:
title: true
date: true
path: true
text: false
raw: false
content: false
slug: false
updated: false
comments: false
link: false
permalink: false
excerpt: false
categories: false
tags: true
小可爱的小可爱，<br/>拖肥的娘亲，<br/>划水的ACMer，<br/>努力中的小菜鸡，<br/>想要自信和一往无前的勇气。