Balanced Sequence (贪心)

Balanced Sequence

题意

给你几个含有左右括号的串，你可以任意组合，求组合能得到的最大的括号匹配数量。

贪心。

具体贪心法可以见代码。

看！代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <bits/stdc++.h>
#pragma comment(linker, “/STACK:1024000000,1024000000”)
using namespace std;
struct node{
    int left_no,right_no,yes;
    node()
    {
        left_no=right_no=yes=0;
    }
};
bool cmp(node a,node b)
{
    if(a.left_no>=a.right_no&&b.left_no<=b.right_no)//左少右多 + 左多右少 a前面
        return true;
    if(a.left_no<=a.right_no&&b.left_no>=b.right_no) //左少右多 + 左多右少 b前面
        return false;
    if(a.left_no<=a.right_no&&b.left_no<=b.right_no) //左少右多+左少右多 谁的左面数量多谁放前面
        return a.left_no>b.left_no;
    return a.right_no<b.right_no; // 左多右少 左多右少 谁的右边多谁放后面

}
char s[5000010];
int main()
{
    int n,t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        vector<node>a(n);
        int len;
        for(int i=0;i<n;i++)
        {
            scanf("%s",s);
            len=strlen(s);
            long long left=0,right=0,ans=0;
            for(int j=0;j<len;j++)
            {
                if(s[j]=='(')
                    left++;
                else
                {
                    if(left>0)  left--,ans++;
                    else    right++;
                }
            }
            a[i].left_no=left;
            a[i].right_no=right;
            a[i].yes=ans;
        }
        sort(a.begin(),a.end(),cmp);
        long long left=0,right=0,ans=0;
        for(int i=0;i<n;i++)
        {
            ans+=a[i].yes;
            if(left>=a[i].right_no)
                left-=a[i].right_no,ans+=a[i].right_no;
            else
                ans+=left,left=0;
            left+=a[i].left_no;
        }
        printf("%lld\n",ans*2);
    }
    return 0;
}

展开全文 >>

Swordsman(多个优先队列)

 Swordsman

题意

给你一个n,代表有n个队伍，一个k，代表每个队伍中有k个战士，对应k个经验值，我方队伍中也有k个战士。

输入我方战士的k个战斗力，

接下来每一行输入敌方每个队伍k个战士的战斗力，打败k个战士后可以得到的经验值。

只有我方k个战士的战斗力均对应大于敌方某个队伍中k个战士的战斗值，才能得到相应的k个经验，提升战斗力，然后接着跟其他的队伍打。

问你我方战士每个人最后最多能为多少战斗力？

k<=5,n<=1e5，保证得到的战斗力在int范围内。

思路

首先由于读入数据大，先来个读入挂。

然后我们可以对每一种敌方战士（列），建立k个优先队列，以战斗值小为上。

然后不断循环，每次从第1个战士开始和第1个队列中的敌方战士打，如果强于他，就弹出这个战士，并记录这个战士对应的队伍中的战败情况，一旦他们的队伍全军覆没，我方每个战士就可以得到相应的经验值，然后和第i个队列中的战士打，一直到i=k为止，结束一轮循环。

然后一直循环直到某一次循环中不再有打赢他们的情况出现。

看！代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
#include <bits/stdc++.h>
using namespace std;
priority_queue<pair<int,int>,vector<pair<int,int> >,greater<pair<int,int> > >a[6];
namespace IO {
    const int MX = 4e7; //1e7 占用内存 11000kb
    char buf[MX]; int c, sz;
    void begin() {
        c = 0;
        sz = fread(buf, 1, MX, stdin);//一次性全部读入
    }
    inline bool read(int &t) {
        while (c < sz && buf[c] != '-' && (buf[c] < '0' || buf[c] > '9')) c++;
        if (c >= sz) return false;//若读完整个缓冲块则退出
        bool flag = 0; if(buf[c] == '-') flag = 1, c++;
        for(t = 0; c < sz && '0' <= buf[c] && buf[c] <= '9'; c++) t = t * 10 + buf[c] - '0';
        if(flag) t = -t;
        return true;
    }
}
int n,k,x,d[6],b[100008][6],c[100008]; //d用来存当前战斗力，b是打败的奖励，c是记录某一行的打败情况
pair<int,int>zz;
int main()
{
    cin.tie(0);
    cout.tie(0);
    int t;
    IO::begin();
    IO::read(t);
    while(t--)
    {
        IO::read(n);
        IO::read(k);
        memset(c,0,sizeof(c));
        for(int i=1;i<=k;i++) IO::read(d[i]);
        for(int i=1;i<=k;i++)
        {
            while(a[i].size()) a[i].pop();
        }
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=k;j++) IO::read(x),zz.first=x,zz.second=i,a[j].push(zz); //先把所有的情况放到优先队列中
            for(int j=1;j<=k;j++) IO::read(b[i][j]);
        }
        int ans=0;
        bool f;
        while(true)
        {
            f=0;
            for(int i=1;i<=k;i++)    //对于每一列
            {
                while(!a[i].empty()) //对于某一列的最小的元素
                {
                    zz=a[i].top();
                    if(zz.first<=d[i])  //可以打败
                    {
                        a[i].pop();
                        c[zz.second]++;  //记录下这一行的打败情况
                        if(c[zz.second]==k) //如果这一行都打败了 ，就吃掉啦
                        {
                            for(int j=1;j<=k;j++) d[j]+=b[zz.second][j];
                            ans++,f=1;
                        }
                    }
                    else break;
                }
            }
            if(!f) break; //如果某次循环中没有能吃的，就break了
        }
        cout<<ans<<endl;
        for(int i=1;i<=k;i++)
        {
            if(i==1) cout<<d[i];
            else cout<<" "<<d[i];
        }
        puts("");
    }
    return 0;
}

展开全文 >>

Age of Moyu(bfs)

Age of Moyu

题意

给你n个点，m条边，要求从1号走到n号，每条边上都有一种颜色，如果你在相同颜色的边上走，不会有额外的花费，但是如果你从一种颜色的边走到另一种颜色的边上，那么就要加1的花费，求的是最小花费。

1<=n<=1e5, 0<=m<=2e5

多组。

思路

如果直接bfs优先队列处理大顶堆的话，把跑过的点或者边标记了的话，是考虑不周到的。

如：

6 8

1 2 2

2 3 2

3 4 2

1 4 1

1 5 1

4 5 2

5 6 2

2 6 1 答案应该是1，但是很多都容易输出2。

正确的做法是，用set[i]储存每次到达点i的前驱结点，如果到达这个点的花费比历史中到达这个点的最小花费要大，就continue,如果相等，前驱结点在set中，continue，如果不在set中，就放入set中，如果小于的话，就把set[i]清空，然后把历史最小花费mincost[i]更新了，并且把前驱结点放到set中（我发现放这条边的颜色也是可以的），然后对当前这个点连出去的每一条边继续判断，如果不是反向边，而且mincost[nxt]>=（(当前颜色!=下个颜色)+mincost[i]），就把mincost[nxt]更新了，并且如果nxt点不是终点，就把nxt点push到优先队列中，优先队列存的是每一个点的到达状态，按照到达的花费从小到大放。

看！代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
#include <bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn =1e5+5;
struct edge{
    int to,color,nxt; //下一个点，这条边的颜色，对于这个点相连的下一条边
}e[maxn<<2];
set<int>preid[maxn]; //到达某点时花费相同的前一个结点
int idcost[maxn]; //到达某点的最小花费
int head[maxn]; //暂时记录上一条边的

struct node{
    int val,id;//当前总花费，当前到达点
    int color,father;//前一条边上的颜色，前一个结点
    bool operator <(const node &p) const{return val>p.val;}
};

int solve(int n)
{
    priority_queue<node>q;
    idcost[1]=0;
    q.push((node){idcost[1],1,-1,-1});
    int len,id,color,father,tot,i,cl,nxt;
    node tmp;
    while(!q.empty())
    {
        tmp=q.top();
        q.pop();
        id=tmp.id,tot=tmp.val,father=tmp.father,color=tmp.color;
        if(tot>idcost[id]) continue; //如果当前到达的总花费比到这一点的最小的花费要贵
        else if(tot==idcost[id])
        {
            if(preid[id].find(color)!=preid[id].end()) //如果当前到达点已经记录了前一个点的颜色//我发现father前驱结点也是对的
                continue;
            preid[id].insert(color);
        }
        else //更新最小花费
        {
            preid[id].clear();
            preid[id].insert(color);
            idcost[id]=tot;
        }
        for(i=head[id];~i;i=e[i].nxt) //对于这个点连接的其他点
        {
            cl=e[i].color;
            nxt=e[i].to;
            if(nxt==father) continue; //反向边
            if(((cl!=color)+idcost[id])<=idcost[nxt])
            {
                idcost[nxt]=(cl!=color)+idcost[id];
                if(nxt!=n)
                    q.push((node){idcost[nxt],nxt,cl,id});
            }
        }
    }
    if(idcost[n]==INF) return -1;
    return idcost[n];
}
int main()
{
#ifndef ONLINE_JUDGE
    freopen("in.txt","r",stdin);
    freopen("out.txt","w",stdout);
#endif
    int n,m;
    int u,v,w;
    while(~scanf("%d%d",&n,&m))
    {
        memset(head,-1,sizeof(head));
        memset(idcost,INF,sizeof(idcost));
        int total=0;
        for(int i=1;i<=n;i++)
            preid[i].clear();
        while(m--)
        {
            scanf("%d%d%d",&u,&v,&w);
            e[total]=(edge){v,w,head[u]}; //一种新型存边方式hhh
            head[u]=total++;
            e[total]=(edge){u,w,head[v]};
            head[v]=total++;
        }
        printf("%d\n",solve(n));
    }
    return 0;
}

展开全文 >>

Sequence(整除分块+矩阵快速幂)

 Sequence

题意

定义：
$$
F_1=A
$$

$$
F_2=B
$$

$$
F_n=D\cdot{}F_{n-1}+C\cdot{}F_{n-2}+\lfloor\frac{P}{n}\rfloor
$$

求Fn，Mod1e9+7。

思路

一看到这个向下取整！

多么亲切啊！

整除分块啊！

……

一开始怎么都想不出来怎么把分块用进去，队友一波机智，先分块，然后矩阵快速幂，哇，秒啊，然后两个小时过去了……

由于莫比乌斯中我们经常会用到一个分块的概念：
$$
\sum_{i=1}^n\lfloor\frac{n}{i}\rfloor
$$

1
2
3
4
5
for(int l=1,r;l<=n;l=r+1)
{
    r=n/(n/l);
    ans+=(r-l+1)*(n/l);
}

那么我们就想，因为矩阵快速幂要求的是尾项是个常数，而对于这个整除来说，在某些区间内它的值是一定的，因此我们就可以先把他们划分为好几块，然后对于每个区间进行矩阵快速幂即可，有些细节注意，比如说次数不足3次时，要手写一波判断，因为没有需要的Fn-1，Fn-2，比如n小于p的时候，需要在循环内直接结束，比如n大于p的时候，分块结束后再进行裸的矩阵快速幂。

看！代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int MOD = 1e9+7;
struct mat
{
    long long a[3][3];
}m,r;
mat mult(mat x,mat y)
{
    mat res={0};
    int i,j,k;
    for(i=0;i<3;i++)
    for(j=0;j<3;j++)
    for(k=0;k<3;k++)
        res.a[i][j]=(res.a[i][j]+(x.a[i][k]*y.a[k][j])%MOD)%MOD;
    return res;
}
mat PowerMod(mat x,long long n)
{
    mat ans={0};
    int i,j;
    for(i=0;i<3;i++)
    ans.a[i][i]=1;
    while(n>0)
    {
        if(n%2==1)
        ans=mult(ans,x);
        x=mult(x,x);
        n=n/2;
    }
    return ans;
}
int main()
{
    int t;
    ll a,b,c,d,p,n;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%lld%lld%lld%lld%lld%lld",&a,&b,&c,&d,&p,&n);
        if(n==1) { printf("%lld\n",a);continue;}
        else if(n==2) { printf("%lld\n",b);continue;}
        m.a[0][2]=m.a[1][1]=m.a[2][1]=m.a[2][0]=0;
        m.a[0][0]=d;m.a[0][1]=c;
        m.a[1][0]=m.a[2][2]=1;
        ll pre=b,ppre=a;
        for(int L=3,R;L<=p;L=R+1)
        {

            R=p/(p/L); 
            int zs=min(1ll*R-L+1,n-L+1);
            if(zs<=3)
            {
                for(int i=1;i<=zs;i++)
                {
                    ll tmp=pre;
                    pre=((pre*d+ppre*c)%MOD+p/L)%MOD;
                    ppre=tmp;
                }
                if(n>=L&&n<=R) break;
                continue;
            }
            m.a[0][2]=p/L;
            r=PowerMod(m,zs);
            ll p1=(r.a[0][0]*pre+r.a[0][1]*ppre+r.a[0][2])%MOD;
            ll p2=(r.a[1][0]*pre+r.a[1][1]*ppre+r.a[1][2])%MOD;
            pre=p1;ppre=p2;
            if(n>=L&&n<=R) break;
        }
        if(n>p)
        {
            m.a[0][2]=0;
            r=PowerMod(m,n-max(2ll,p));
            ll p1=(r.a[0][0]*pre+r.a[0][1]*ppre+r.a[0][2])%MOD;
            pre=p1;
        }
        printf("%lld\n",pre);
    }
    return 0;
}

展开全文 >>

Family View（AC自动机求匹配串位置）

# Family View

题意

就是给你n个模式串，长度总和不超过1e6，给你一个匹配串，长度不超过1e6，然后要求是把匹配的字符换成”*”。

思路

AC自动机，在标记尾节点的地方（个数）顺带标记一下匹配串的最长长度，然后用vector pair存一下每次匹配时的位置和匹配的长度，最后对于每一pair进行处理。（对了 先把模式串用小写的保存下来，因为不区分大小写）

看！代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
//该程序不能判别相同模式串，因此若模式串重复，答案会将相同模式串当做不同的处理，因此若需要可以用map去重或修改insert
#include<bits/stdc++.h>
using namespace std;
const int maxm=1000006;    //maxm是总结点数：约为字母数+++

char S[maxm],word[maxm];
char s2[maxm];
struct node{
    int tail;
    int len;
}tt[maxm];
int nxt[maxm][26],f[maxm],size;    //nxt是结点指向不同字母的结点下标，tail是表示该结点为几个单词的词尾(可能需要计算重复的模式串情况),f是当不匹配时转跳到的结点下标,size是结点数
vector<pair<int,int> >Index; //位置、长度

int newnode(){    //初始化整个trie或建立新的结点时，首先初始化当前结点所指向的26个字母的结点为0，表示暂时还没有指向的字母，然后暂定该结点不是单词尾结点，暂无失配时转跳位置（即转跳到根节点），返回结点标号
    memset(nxt[size],0,sizeof(nxt[size]));
    f[size]=tt[size].tail=0;
    tt[size].len=0;
    return size++;
}

void insert(char s[]){    //构造trie,p为当前结点的上一个结点标号，初始为0；x即为当前结点（上个结点标号指向当前字母的结点）标号,若此结点还未出现过，那么就建立这个结点；然后更新p为当前结点标号以便后续操作
    int i,p=0;
    for(i=0;s[i];i++){
        int &x=nxt[p][s[i]-'a'];
        p=x?x:x=newnode();
    }
    tt[p].tail++;    //此时仅将s串记录，即将s串结尾的结点加1，若无相同模式串，则此操作只会使所有串尾结点的tail值由0变为1，但有相同模式串，则会重复记录，需要去重可以用map或用tail[p]=1;语句来完成
    tt[p].len=max(tt[p].len,(int)strlen(s));
}

void makenxt(){    //利用bfs来构造失配指针
    int i;
    queue<int>q;
    f[0]=0;    //先将0结点挂的字母加入队列，失配指针指向0结点
    for(i=0;i<26;i++){
        int v=nxt[0][i];
        if(v){
            f[v]=0;
            q.push(v);
        }
    }
    while(!q.empty()){
        int u=q.front();
        q.pop();
        for(i=0;i<26;i++){
            int v=nxt[u][i];
            if(!v)nxt[u][i]=nxt[f[u]][i];    //当u结点没有i对应字母，则视为失配，将其指向失配后转跳到的结点所指向的i对应字母
            else{
                q.push(v);    //u结点存在指向i的结点，则将所指向的结点下标加入队列
                f[v]=nxt[f[u]][i];    //失配指针指向上个结点失配指针指向结点所挂当前字母的结点
            }
        }
    }
}

int query(char s[]){    //查询s串中模式串出现了多少种/次
    int ans=0,v=0;
    for(int i=0;s[i];i++){
        while(v&&!nxt[v][s[i]-'a'])v=f[v];    //先匹配直到没有失配
        v=nxt[v][s[i]-'a'];
        int tmp=v;
        while(tmp){
            if(tt[tmp].tail!=0) //这里！
                Index.push_back(make_pair(i,tt[tmp].len));
            tmp=f[tmp];
        }
    }
    return ans;
}

int main()
{
    int T;
    scanf("%d",&T);
    while(T--)
    {
        Index.clear();
        int n;
        scanf("%d",&n);
        size=0,newnode();
        for(int i=0;i<n;i++)
        {
            scanf("%s",word);
            insert(word);
        }
        makenxt();
        getchar();
        gets(S);
        int len=strlen(S);
        for(int i=0;i<len;i++)
            if(S[i]>='A'&&S[i]<='Z')
                s2[i]=S[i]-'A'+'a';
            else
                s2[i]=S[i];
        query(s2);
        len=Index.size();
        for(int i=0;i<len;i++)
  	    {
            for(int j=0;j<Index[i].second;j++)
                S[Index[i].first-j]='*';
        }
        puts(S);
    }
    return 0;
}

AC自动机注释模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
//该程序不能判别相同模式串，因此若模式串重复，答案会将相同模式串当做不同的处理，因此若需要可以用map去重或修改insert
#include<stdio.h>
#include<string.h>
#include<queue>
using namespace std;
const int maxm=500006;    //maxm是总结点数：约为字母数+++

char s[1000005],word[55];
int nxt[maxm][26],tail[maxm],f[maxm],size;    //nxt是结点指向不同字母的结点下标，tail是表示该结点为几个单词的词尾(可能需要计算重复的模式串情况),f是当不匹配时转跳到的结点下标,size是结点数

int newnode(){    //初始化整个trie或建立新的结点时，首先初始化当前结点所指向的26个字母的结点为0，表示暂时还没有指向的字母，然后暂定该结点不是单词尾结点，暂无失配时转跳位置（即转跳到根节点），返回结点标号
    memset(nxt[size],0,sizeof(nxt[size]));
    f[size]=tail[size]=0;
    return size++;
}

void insert(char s[]){    //构造trie,p为当前结点的上一个结点标号，初始为0；x即为当前结点（上个结点标号指向当前字母的结点）标号,若此结点还未出现过，那么就建立这个结点；然后更新p为当前结点标号以便后续操作
    int i,p=0;
    for(i=0;s[i];i++){
        int &x=nxt[p][s[i]-'a'];
        p=x?x:x=newnode();
    }
    tail[p]++;    //此时仅将s串记录，即将s串结尾的结点加1，若无相同模式串，则此操作只会使所有串尾结点的tail值由0变为1，但有相同模式串，则会重复记录，需要去重可以用map或用tail[p]=1;语句来完成
}

void makenxt(){    //利用bfs来构造失配指针
    int i;
    queue<int>q;
    f[0]=0;    //先将0结点挂的字母加入队列，失配指针指向0结点
    for(i=0;i<26;i++){
        int v=nxt[0][i];
        if(v){
            f[v]=0;
            q.push(v);
        }
    }
    while(!q.empty()){
        int u=q.front();
        q.pop();
        for(i=0;i<26;i++){
            int v=nxt[u][i];
            if(!v)nxt[u][i]=nxt[f[u]][i];    //当u结点没有i对应字母，则视为失配，将其指向失配后转跳到的结点所指向的i对应字母
            else{
                q.push(v);    //u结点存在指向i的结点，则将所指向的结点下标加入队列
                f[v]=nxt[f[u]][i];    //失配指针指向上个结点失配指针指向结点所挂当前字母的结点
            }
        }
    }
}

int query(char s[]){    //查询s串中模式串出现了多少种/次
    int ans=0,v=0;
    for(int i=0;s[i];i++){
        while(v&&!nxt[v][s[i]-'a'])v=f[v];    //先匹配直到没有失配
        v=nxt[v][s[i]-'a'];
        int tmp=v;
        while(tmp){
            ans+=tail[tmp];
            tail[tmp]=0;    //这里加这句是为了仅计算出现多少种模式链，而若不加这句则可以计算累计出现多少次
            tmp=f[tmp];
        }
    }
    return ans;
}

int main(){
    int T;
    scanf("%d",&T);
    while(T--){
        int n;
        scanf("%d",&n);
        size=0,newnode();
        for(int i=0;i<n;i++){
            scanf("%s",word);
            insert(word);
        }
        makenxt();
        scanf("%s",s);
        printf("%d\n",query(s));
    }
    return 0;
}

结构体版

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
#include<iostream> //查询匹配的数量 ，不知道有没有带重复的
#include<cstdio>
#include<queue>
#include<cstring>
using namespace std;

struct asd{
    int fail; // 失配指针
    int vis[26]; // 子节点的位置
    int end; // 标记有几个单词以这个节点结尾 
} AC[1000010];
int rt,cnt,l,n;
char ch[1000010];

inline void build(char *ch)
{
    int l=strlen(ch+1);
    int now=rt,v;
    for(int i=1;i<=l;i++)
    {
        v=ch[i]-'a';
        if(!AC[now].vis[v]) AC[now].vis[v]=++cnt;
        now=AC[now].vis[v];
    }
    AC[now].end+=1;
}

inline void get_fail()
{
    queue <int> Q;
    for(int i=0;i<=25;i++) // 第一层肯定没有之前的点与他匹配 
        if(AC[rt].vis[i]) 
            Q.push(AC[rt].vis[i]); // 因为默认是 0 所以没有写指向根节点 
    while(!Q.empty())
    {
        int u=Q.front(); Q.pop();
        for(int i=0;i<=25;i++) // 枚举所有子节点
        {
            if(AC[u].vis[i]) // 存在这个子节点
            {
                AC[AC[u].vis[i]].fail=AC[AC[u].fail].vis[i];
                // 子节点的fail指针指向当前节点的
                // fail指针所指向的节点的相同子节点 
                Q.push(AC[u].vis[i]);
            }
            else //不存在这个子节点
            AC[u].vis[i]=AC[AC[u].fail].vis[i];
            // 当前节点的这个子节点指向当
            // 前节点fail指针的这个子节点 
        }
    }
}

inline int query(char *ch)
{
    int l=strlen(ch+1);
    int now=rt,ans=0,u;
    for(int i=1;i<=l;i++)
    {
        u=ch[i]-'a';
        now=AC[now].vis[u];
        for(int j=now; j && AC[j].end!=-1; j=AC[j].fail)
        {
            ans+=AC[j].end;
            AC[j].end=-1;
        }
    }
    return ans;
}

int main()
{
    cin>>n;
    for(int i=1;i<=n;i++)
    {
        scanf("%s",ch+1);
        build(ch);
    }
    get_fail();
    scanf("%s",ch+1);
    printf("%d\n",query(ch));
    return 0;
}

展开全文 >>

GuGuFishtion(欧拉函数公式+莫比乌斯)

GuGuFishtion

题意

求：
$$
Ans=\sum_{i=1}^{n}\sum_{j=1}^m\frac{φ(ij)}{φ(i)φ(j)}%p
$$
其中，n,m<=1e6, max(n,m)<=p<=1e9，且p为素数。

##思路

由欧拉函数公式：
$$
φ(x)=x(1-\frac{1}{p_1})(1-\frac{1}{p_2})(1-\frac{1}{p_3})…(1-\frac{1}{p_n})，其中p_i为x的质因子
$$
将公式带入$\frac{φ(ij)}{φ(i)φ(j)}$中：
$$
原式=\frac{ij(1-\frac{1}{c_1})…(1-\frac{1}{c_t})}{i(1-\frac{1}{a_1})…(1-\frac{1}{a_n})j(1-\frac{1}{b_1})…(1-\frac{1}{b_m})}
$$

$$
=\frac{1}{(1-\frac{1}{a_1})(1-\frac{1}{a_2})…(1-\frac{1}{b_1})(1-\frac{1}{b_2})…}
$$

上下同乘以gcd(i,j)，则可以得到：

(这里虽然讲不清楚但是大致是一个容斥)
$$
原式=\frac{gcd(i,j)}{gcd(i,j)-gcd(i,j)/质因数的任意组合+gcd(i,j)/所有质因子的组合}
$$

$$
=\frac{gcd(i,j)}{φ(gcd(i,j))}
$$

因此
$$
Ans=\sum_{i=1}^{n}\sum_{j=1}^m\frac{gcd(i,j)}{φ(gcd(i,j))}%p
$$
令k=gcd(i,j)，并枚举k，有：
$$
Ans=\sum_{i=1}^{n}\sum_{j=1}^m\sum_{k=1}^{min(n,m)}\frac{k}{φ(k)}[gcd(i,j)==k]%p
$$

$$
=\sum_{k=1}^{min(n,m)}\frac{k}{φ(k)}\sum_{i=1}^{n}\sum_{j=1}^m[gcd(i,j)==k]%p
$$

$$
=\sum_{k=1}^{min(n,m)}\frac{k}{φ(k)}\sum_{i=1}^{\lfloor\frac{n}{k}\rfloor}\sum_{j=1}^{\lfloor\frac{m}{k}\rfloor}[gcd(i,j)==1]%p
$$

$$
=\sum_{k=1}^{min(n,m)}\frac{k}{φ(k)}\sum_{i=1}^{\lfloor\frac{n}{dk}\rfloor}\sum_{j=1}^{\lfloor\frac{m}{dk}\rfloor}
\sum_{d=1}^{min(n,m)}μ(d)%p
$$

$$
=\sum_{k=1}^{min(n,m)}\frac{k}{φ(k)}\sum_{d=1}^{min(n,m)}μ(d){\lfloor\frac{n}{dk}\rfloor}{\lfloor\frac{m}{dk}\rfloor}%p
$$

就可以做啦！

枚举k=1~min(n,m)，先分析出要预先求的东西：

  1. μ(d)
  2. φ(k)

预处理：由于n/dk向下取整时，当dk>n，值为0，因此我们只要先枚举dk=1到min(n,m)即可。

然后对于for(k)，dk为d的倍数增长，此时，d=dk/k,将μ(dk/k)、n/dk、m/dk相乘，取模得到F(k)+=。

计算：然后就可以一个大循环，枚举k从1~min(n,m)，求得k*逆元(φ(k))，再*先前求得的F(k)，并取模即可。

注意：由于时间限制， 取模一定要尽量少取。特别是在预处理阶段中，求F(k)时，由于F(k)是重复累加的，因此若是每一次累加都取模，会造成不必要的时间浪费，因此我们可以把F(k)开long long，然后在全部预处理完毕之后再一次性for取模。

看！代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
ll MOD;
const int maxn = 1000000 + 5;
int phi[maxn],mu[maxn],prim[maxn];
bool vis[maxn]={0};

ll quzheng[maxn],f[maxn];
int cnt=0;
ll ex_gcd(ll a,ll b,ll &x,ll &y)//扩展欧几里得（扩展gcd）
{
	if (a==0&&b==0) return -1;
	if (b==0){x=1;y=0;return a;}
	ll d=ex_gcd(b,a%b,y,x);
	y-=a/b*x;
	return d;
}

ll mod_inverse(ll a,ll n)//乘法逆元，a与n必须互素
{
	ll x,y;
	ll d = ex_gcd(a,n,x,y);
	return (x%n+n)%n;
}

/** 对于μ函数的线筛 */
void get_mu(int n)
{
    mu[1]=phi[1]=1;
	for(int i=2;i<=n;i++)
	{
    	if(!vis[i]){prim[++cnt]=i;mu[i]=-1;phi[i]=i-1;}
   	 	for(int j=1;j<=cnt&&prim[j]*i<=n;j++)
        {
        	vis[prim[j]*i]=1;
        	if(i%prim[j]==0) {phi[i*prim[j]]=phi[i]*prim[j];break;}
        	else {mu[i*prim[j]]=-mu[i];phi[i*prim[j]] = phi[i] * phi[prim[j]];}
    	}
	}

}

int cal(int n,int m)
{
    memset(f,0,sizeof(f));
    int MIN=min(n,m);
    for(int i=1;i<=MIN;i++) quzheng[i]=1ll*(n/i)*(m/i);
    for(int i=1;i<=MIN;i++)
        for(int j=i;j<=MIN;j+=i)
            f[i]+=1ll*mu[j/i]*quzheng[j];
    for(int i=1;i<=MIN;i++) //就是这个TLE
        f[i]%=MOD;
}

int main()
{
    int n,m,t;
    get_mu(1000000);
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d%lld",&m,&n,&MOD);
        cal(n,m);
        int MIN=min(n,m);
        ll ans=0;
        for(int i=1;i<=MIN;i++)
        {
            ans=(ans+(1ll*i*mod_inverse(phi[i],MOD))%MOD*f[i]+MOD)%MOD;
        }
        printf("%lld\n",ans);
    }
    return 0;
}

展开全文 >>

Recovery(构造)

## Recovery

题意

给两行，由01组成，一行表示行中1的个数，一行表示列中1的个数，奇数为1，偶数为0。

如果不能构造就是-1，能就输出原来的矩阵的样子。

按照1尽可能的多，然后字典序小。

思路

不太好说，这个。。。。就。。。看代码吧。

主要是发现行列之间1的关系，以及如何放比较好，。

看！代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
#include <bits/stdc++.h>
using namespace std;
int main()
{
    string hang;
    string lie;
    cin>>hang>>lie;
    int h[55],l[55];
    int lenh,lenl;
    int cnth=0,cntl=0;
    lenh=hang.size(),lenl=lie.size();
    for(int i=0;i<lenh;i++)
    {
        if(hang[i]=='0'&&lenl%2==0||hang[i]=='1'&&lenl%2==1)
            h[i]=0;
        else h[i]=1,cnth++;
    }
    for(int i=0;i<lenl;i++)
    {
        if(lie[i]=='0'&&lenh%2==0||lie[i]=='1'&&lenh%2==1)
            l[i]=0;
        else l[i]=1,cntl++;
    }
    if(cnth%2!=cntl%2)
    {
        printf("-1\n");return 0;
    }
    int i=0;
    while(cnth<cntl)
    {
        if((h[i]+2)<=lenl) h[i]+=2,cnth+=2;
        else i++;
    }
    i=0;
    while(cnth>cntl)
    {
        if((l[i]+2)<=lenh) l[i]+=2,cntl+=2;
        else i++;
    }
    for(i=0;i<lenh;i++)
    {
        for(int j=0;j<lenl;j++)
        {
            if(h[i]!=0&&l[j]!=0)
            {
                h[i]--,l[j]--;
                printf("0");
            }
            else printf("1");
        }
        printf("\n");
    }
    return 0;
}

展开全文 >>

Bramasole

白色恋人，浪漫的意大利男性，治愈的开始，另一场人生的结束

“我把集市上买的一颗热葡萄塞进嘴里，肆意的甜蜜在口腔蔓延，甚至闻起来也是紫色的。”

这大概是在整部电影中让我印象最深刻的一句话了。

在徐志摩先生笔下，佛罗伦萨（翡冷翠）是有风穿过橄榄林带来着石榴花香，蓝天白云下有色彩鲜艳的隔壁，深绿色的百叶窗和深红色的屋顶，隔着夜，隔着天，通着恋爱的灵犀一点。旅行、到一个五颜六色的地方，认识五颜六色的陌生人。在看完这部电影之后，我几乎就想即刻动身了。我知道有这么一个地方，它有充足的阳光，适合葡萄生长，也适合酿造爱情和生活，“当太阳照在山顶上的伊特鲁里亚石壁上，洋槐树就被镶上金边，色彩柔和的房子沿着小河岸弯弯曲曲的排列，如同水彩画一般”，“微风吹拂的白色窗帘，墙角灰白色的陶罐，麦田里新收的草卷儿”。我希望一动不动的盯着这片土地，天旋地转。旅行的魅力。

而托斯卡纳的乡野，总会使人联想起高更、梵高那些大师们的画笔，大片大片浓厚的色彩，金色的、橘色的、紫罗兰色的，这般会流动的色彩。语言在其面前是多么苍白。如果可以，我甚至想把那些灿烂的色彩贴在这张白纸上。像墨绿的火焰一样朝向天空的树林，金光流溢的草原，盛开的虞美人，色彩的盛宴。

这里有达芬奇，有文艺复兴，还有郁郁葱葱长满葡萄藤的山坡。

然后弗兰西斯来到了这里。

在明信片上写下了“紫色”的心情，开始改变，是托斯卡纳送给她的第一份礼物。

原本只是一场失意的旅行，却用自己所有的积蓄买下了一座破败不堪的，连水龙头都出不了水的小房子——“Bramasole”，意大利语向往阳光的意思。命运的突然就像是在“Bramasole”中被白鸽的粪便砸中，而过去就像海中突然陆沉的岛屿，一下子消失不见了。然后一切就成真了。新生活是具体的，一砖一瓦，雕花的铁床，栏杆上的画像，刚刚成熟的橄榄，从此她拥有“三口水井、一条罗马古道、一处伊特拉斯坎人的古城墙遗址、一条地下信道、一百一十七棵橄榄树、二十棵李树、以及其他数也数不清处的果树和花丛，还可以在屋外铺着亚麻布的长桌上，吃着用院子里才来的鼠尾草做馅料的意大利方饺，敲开路边捡来的球果、用其中的松仁做出香味四溢的老祖母馅饼……”这座房子实在是太老了，就像你会随时倒下去长眠不醒的老祖母。

而生活就是与人不停的邂逅，不停的与周边的环境发生关系。

在她落寞绝望时充满耐心的安慰她的可靠的房产中介，靠美和灵性生活，永远纯真如孩童叫她振作起来的神秘女郎，帮法兰西斯修房子的修缮工们，还有每天早晨为路边的圣母像献上鲜花，悼念亡妻的老人，以及属于她的一场短暂的罗曼蒂克史。

一点一点回移的日子就好像小野丽莎的歌，fly me to the moon，柔柔软软轻轻悄悄的，不经意而温柔的掠过。

治愈是我所有能形容这部电影的词汇。

其实那个时候刚好是我生活的极大转折点——一个不知道会往哪里转向的，不知是褒义还是贬义的转折点。说不知道，但当时的我，连呼吸都是不知所措。在不愿意接受的悲伤中也思考生活的方向，我知道我为什么不愿意接受这样的转折，尽管它的本质是好的。就像弗兰西斯，离婚也是她不愿意接受的事实，是很难走出来的人生巨大的转折点。在这样的时刻，往往所有的注意力会被吸引，会失去对其他事物的热情，天晴的时候在下雨，下雨的时候整个人都会湿透。弗兰西斯在忙碌琐碎的装修之中顾不及心碎的滋味，但我一静下来，手头空空荡荡的时候，各种情绪翻江倒海的来了，落魄不止。

我听到弗兰西斯一个人的嘶喊：

“我一个人住那么大的房子有什么用？”

那你为什么还要在这里？

“因为我厌倦了恐惧，因为我的心底仍然有希望。”

“我想要在这里举办一场婚礼，我想要有一个家。”

有时候遇到很糟糕的境遇，躲不开、避不掉的重重压力围城，生活被就像被胡乱泼了墨。在这个时候，希望是最美好的东西。

好心的中介讲了这么一个故事，他说奥地利和意大利之间的阿尔卑斯山脉中有一段叫做塞默灵，那段山脉地势险峻，令人望而生畏，他们在那里建造了连通维也纳和威尼斯的铁路。尽管当时根本没有火车可以驶过，但他们依然把铁轨铺好了，因为他们知道总有一天会有火车驶过。

你不必期待、不必翘首以盼，该来的总会来，而你，只需要做好准备。

杨绛先生说：“人的一切痛苦本质上都是对自己无能的愤怒。”有时候我们不快乐，是因为想要的太多，希望一切都在自己的手里。但是又何必呢，我们掌握不了的东西就任其流浪，有一句很俗很俗的话讲，该来的总会来。“当我还是个小女孩时，我总是数小时地看瓢虫，最后，我会放弃，然后在草地上睡着了。当我醒来的时候，它们爬得我满身都是。”

影片的最后，弗兰西斯的愿望在托斯卡纳实现了。她想要一个家，托斯卡纳给了她一个靠自己撑起来的家；她想要一场婚礼，一对漂亮真挚的小爱人在她的家里举办了婚礼；她想要孩子，她的好友带着自己刚出世的宝宝和自己的同性恋人来她的房子度假。她想要的一切都有了，只是换了一种方式。

最终，屋子里干涸的水龙头会有潺潺的流水，而好事总会来到，而当它来晚时，也不失为一种惊喜。

“希望你也在这里。”

展开全文 >>

2018暑期训练题解

7.7 [BAPC 2014 Preliminary](https://www.jisuanke.com/contest/1403)

A. 思维题，重点在于当剩余的n<k时，只要k%n==0就可以成功，比如 64 6的时候，先约分：32：6，再约：16:6，一直约到 1:6 ，那n=1，当然ok。

B. dijkstra最短路一下

D. Dp，结束后想了一下，dp[i]表示第i层停下来的所有怨气，dp[i]=min(dp[i],dp[j] + val(j->i)) ,（j<i）i之前电梯停在j层，然后从j直接到i 的话，加上这一部分的怨气就好了val，而valij的怨气就是i的前缀和加上若每一层都停的怨气，再减去了j层停下来的人消失的这部分怨气。

20180712A

F. 飞行航道 水

J. 找单词，八方找，正反找。看了题解 好像是先判断了一下回文减少了一下长度？

7.10 [ Benelux Algorithm Programming Contes](https://www.jisuanke.com/contest/1404)

B. 最少按下的按钮次数

用bfs，时间小于0，变成0，大于3600，变为3600。vis[i]记录时间为i的最少步骤数目。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <bits/stdc++.h>
using namespace std;
const int N=110;
int n,sum;
int a[20],vis[3610];
struct node{
    int val;
    int step;
};
void solve()
{
    queue<node>q;
    node temp,tp;
    temp.val=0;
    temp.step=0;
    q.push(temp);
    vis[0]=0;
    while(!q.empty())
    {
        temp=q.front();
        q.pop();
        for(int i=0;i<n;i++)
        {
            int cur=temp.val+a[i];
            if(cur<0) cur=0;
            else if(cur>3600) cur=3600;
            if(vis[cur]==-1)
            {
                vis[cur]=temp.step+1;
                tp.step=temp.step+1;
                tp.val=cur;
                q.push(tp);
            }
        }
    }
}
int main()
{
    int t;

    scanf("%d",&t);
    while(t--)
    {
        scanf("%d%d",&n,&sum);
        for(int i=0;i<n;i++)
            scanf("%d",&a[i]);
        memset(vis,-1,sizeof(vis));
        solve();
        for(int i=sum;i<=3600;i++)
            if(vis[i]!=-1)
        {
            printf("%d %d\n",vis[i],i-sum);
            break;
        }
    }
    return 0;
}

G. 水

I. 计算组成n的最小的两个斐波那契数a b，其中按b小来排，且a<b

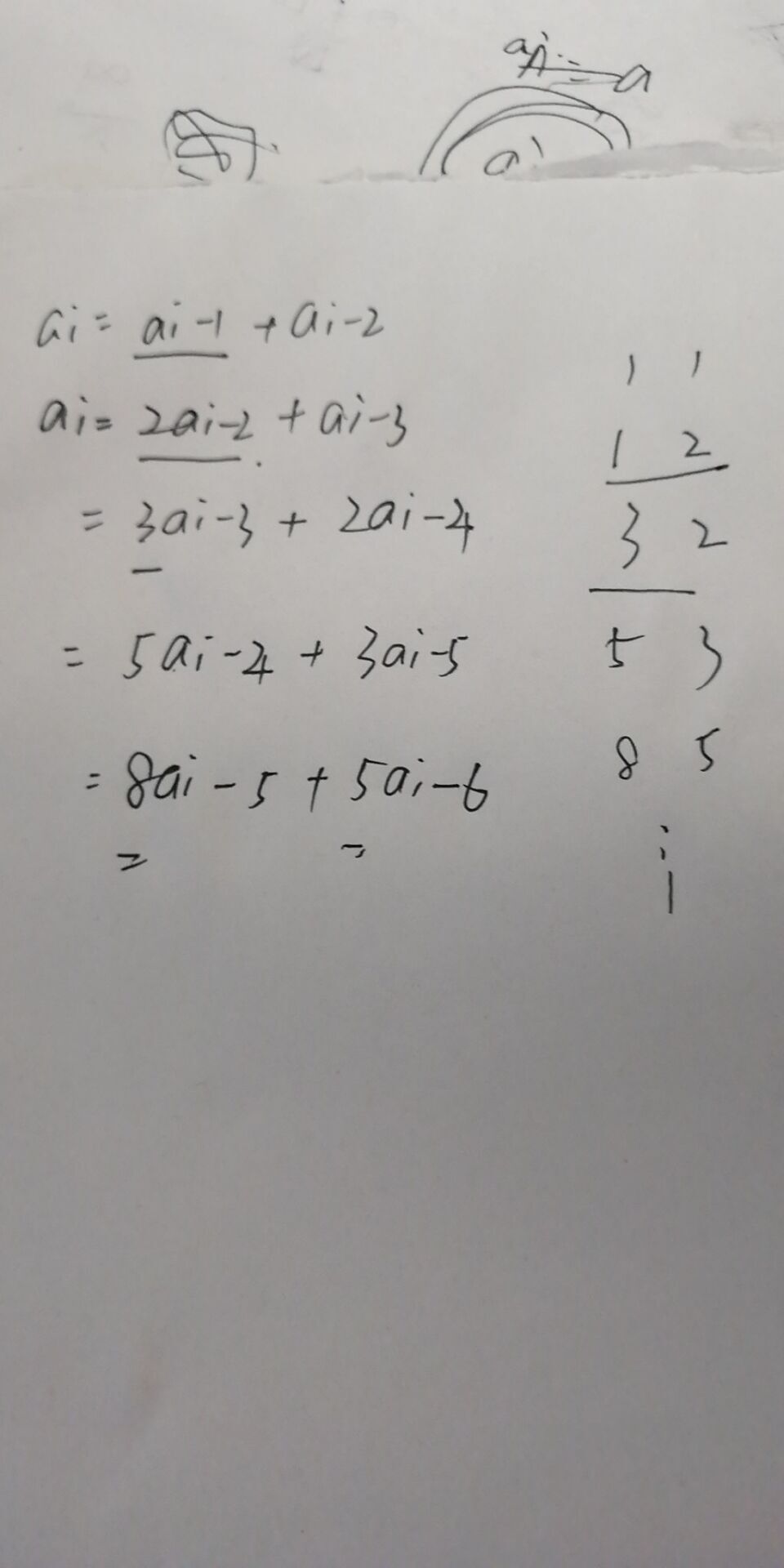
180710I.jpg

由上可知，先计算出最大的两个相邻数相加小于n的地方，设为x，y（x<y），然后xa+yb=n,从b=1开始求满足条件的a，且a<b。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
#include <bits/stdc++.h>
using namespace std;
int a[1000];
const int INF=0x3f3f3f3f;
int main()
{
    a[0]=a[1]=1;
    for(int i=2;i<44;i++)
        a[i]=a[i-1]+a[i-2];
    //小于1e9的斐波那契
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n;
        scanf("%d",&n);
        int loc;
        //计算出最大的两个相邻数相加小于n的地方
        for(int i=43;i>=1;i--)
        {
            if((a[i]+a[i-1])<=n)
            {
                loc=i;break;
            }
        }
        int ai_1;
        while(loc>0)
        {
            for(int i=1;i*a[loc]<n;i++)
            {
                if((n-a[loc]*i)%a[loc-1]==0&&(n-a[loc]*i)/a[loc-1]<=i)
                {
                    ai_1=i;goto out;
                }
            }
            loc--;
        }
    out:
        printf("%d %d\n",(n-a[loc]*ai_1)/a[loc-1],ai_1);
    }
    return 0;
}

J. 把迷宫设置大，然后从中间模拟

7.12

B. 最小路径覆盖，网络流，最大流

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
#include <bits/stdc++.h>
using namespace std;
const int N=5010;
const int M=3000010;
const int inf=0x3f3f3f3f;
struct Edge
{
    int v,cap,nxt;
}e[M];;//邻接表要开边数的两倍
int src,des,dis[N],head[N],ecnt;  //memset dis,head-1 ecnt=0,src=0,des=2*n+1;
int n,m;
void Addedge(int u,int v,int w)
{
    e[ecnt].v=v;
    e[ecnt].cap=w;
    e[ecnt].nxt=head[u];
    head[u]=ecnt++;
    e[ecnt].v=u;
    e[ecnt].cap=0;
    e[ecnt].nxt=head[v];
    head[v]=ecnt++;
}
bool Bfs()
{
    queue<int>q;
    q.push(src);
    memset(dis,-1,sizeof(dis));
    dis[src]=0;
    while(!q.empty())
    {
        int u=q.front();q.pop();
        for(int i=head[u];~i;i=e[i].nxt)
        {
            int v=e[i].v;
            if(e[i].cap>0&&dis[v]==-1)
            {
                dis[v]=dis[u]+1;
                q.push(v);
            }
        }
    }
    return dis[des]>=0;
}
int Dfs(int u,int a)
{
    if(u==des) return a;
    for(int i=head[u];~i;i=e[i].nxt)
    {
        int v=e[i].v,t=0;
        if(e[i].cap>0&&dis[v]==dis[u]+1&&(t=Dfs(v,min(a,e[i].cap))))
        {
            e[i].cap-=t;
            e[i^1].cap+=t;
            return t;
        }
    }
    dis[u]=-1;
    return 0;
}
int Dinic()
{
    int ans=0;
    while(Bfs())
    {
        int t=0;
        while(t=Dfs(src,inf)) ans+=t;
    }
    return ans;
}
int main()
{
    int num,u,v;
    ecnt=0;
    memset(head,-1,sizeof(head));
    scanf("%d",&num);
    src=0;des=2*num+1;
    for(int i=1;i<=num;i++)
        Addedge(0,i,1);
    for(int i=num+1;i<=2*num;i++)
        Addedge(i,2*num+1,1);
    for(int i=1;i<=num;i++)
    {
        scanf("%d",&u);
        while(u--)
        {
            scanf("%d",&v);
            Addedge(i,num+v+1,1);
        }
    }
    n=num+2;
    printf("%d\n",num-Dinic());
    return 0;
}

E. 求次短路是否等于最短路长。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include <cstdio>
#include <cstring>
#include <queue>
#include <algorithm>
#define MAXN (10000 + 10)
#define INF (5000*5000*2)
using namespace std;

struct edge
{
    int to, cost;
    edge(int tv = 0, int tc = 0):
        to(tv), cost(tc) {}
};
typedef pair<int,int> P;
int N, R;
vector<edge> graph[MAXN];
int dist[MAXN];     //最短距离
int dist2[MAXN];    //次短距离

void solve()
{
    fill(dist, dist+N, INF);
    fill(dist2, dist2+N, INF);
    //从小到大的优先队列
    //使用pair而不用edge结构体
    //是因为这样我们不需要重载运算符
    //pair是以first为主关键字进行排序
    priority_queue<P, vector<P>, greater<P> > Q;
    //初始化源点信息
    dist[0] = 0;
    Q.push(P(0, 0));
    //同时求解最短路和次短路
    while(!Q.empty())
    {
        P p = Q.top();
        Q.pop();
        //first为s->to的距离，second为edge结构体的to
        int v = p.second, d = p.first;
        //当取出的值不是当前最短距离或次短距离，就舍弃他
        if(dist2[v] < d) continue;
        for(unsigned i = 0; i < graph[v].size(); i++)
        {
            edge &e = graph[v][i];
            int d2 = d + e.cost;
            if(dist[e.to] > d2)
            {
                swap(dist[e.to], d2);
                Q.push(P(dist[e.to], e.to));
            }
            if(dist2[e.to] > d2 && dist[v] < d2)
            {
                dist2[e.to] = d2;
                Q.push(P(dist2[e.to], e.to));
            }
        }
    }
}
int main()
{
    int A, B, D,K;
    scanf("%d%d%d", &N, &R,&K);
    while(K--)
        scanf("%d",&A);
    for(int i = 0; i < R; i++)
    {
        scanf("%d%d%d", &A, &B, &D);
        graph[A-1].push_back(edge(B-1, D));
        graph[B-1].push_back(edge(A-1, D));
    }
    solve();
    if(dist2[N-1]==dist[N-1])
        printf("yes\n");
    else
        printf("no\n");
    return 0;
}

F. 求大数因子个数，用大数分解求出质因数

7-12German Collegiate Programming Contes…

7-14 https://www.jisuanke.com/contest/1444

7-17The 2018 ACM-ICPC Chinese Collegiate…

7-19 German Collegiate Programming Contes…

7.23 [多校1 ](http://acm.hdu.edu.cn/contests/contest_show.php?cid=802)

1001 Maximum Multiple 水。

1002  Balanced Sequence 贪心题。对于左右括号的情况分类，然后按照规则排序。具体见代码。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
#include <bits/stdc++.h>
#pragma comment(linker, “/STACK:1024000000,1024000000”)
using namespace std;
struct node{
    int left_no,right_no,yes;
    node()
    {
        left_no=right_no=yes=0;
    }
};
bool cmp(node a,node b)
{
    if(a.left_no>=a.right_no&&b.left_no<=b.right_no)//左少右多 + 左多右少 a前面
        return true;
    if(a.left_no<=a.right_no&&b.left_no>=b.right_no) //左少右多 + 左多右少 b前面
        return false;
    if(a.left_no<=a.right_no&&b.left_no<=b.right_no) //左少右多+左少右多 谁的左面数量多谁放前面
        return a.left_no>b.left_no;
    return a.right_no<b.right_no; // 左多右少 左多右少 谁的右边多谁放后面

}
char s[5000010];
int main()
{
    int n,t;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%d",&n);
        vector<node>a(n);
        int len;
        for(int i=0;i<n;i++)
        {
            scanf("%s",s);
            len=strlen(s);
            long long left=0,right=0,ans=0;
            for(int j=0;j<len;j++)
            {
                if(s[j]=='(')
                    left++;
                else
                {
                    if(left>0)  left--,ans++;
                    else    right++;
                }
            }
            a[i].left_no=left;
            a[i].right_no=right;
            a[i].yes=ans;
        }
        sort(a.begin(),a.end(),cmp);
        long long left=0,right=0,ans=0;
        for(int i=0;i<n;i++)
        {
            ans+=a[i].yes;
            if(left>=a[i].right_no)
                left-=a[i].right_no,ans+=a[i].right_no;
            else
                ans+=left,left=0;
            left+=a[i].left_no;
        }
        printf("%lld\n",ans*2);
    }
    return 0;
}

1003 Triangle Partition 水。 对x,y按照升序排序再每次取三个就好了。

1004  Distinct Values 给你一个n，一个q，表示数列中有n个元素，q个区间询问，每次一个[l,r]，表示此区间内的数字不能有重复，要求输出最小字典序的。用set维护一下区间内的数字出现情况就好了。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <bits/stdc++.h>
using namespace std;
bool cmp(pair<int,int>a,pair<int,int>b)
{
    if(a.first==b.first)
        return a.second>b.second;
    return a.first<b.first;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n,q,l,r;
        scanf("%d%d",&n,&q);
        set<int>val;
        vector<pair<int,int> >p;
        vector<int>x(n+5);
        for(int i = 1 ;i <= n ; i++)
            p.push_back( make_pair(i,i) );
        for(int i=1;i<=n;i++)
            val.insert(i);
        for(int i=1;i<=n;i++)
            x[i]=1;
        for(int i=0;i<q;i++)
        {
            scanf("%d%d",&l,&r);
            p.push_back(make_pair(l,r));
        }
        sort(p.begin(),p.end());
        int left=1,cur=1;
        set<int>::iterator it,bef;
        for(int i=0;i<p.size();i++)
        {
            while(left<p[i].first)
                val.insert(x[left++]);
            for(it=val.begin();it!=val.end()&&cur<=p[i].second;)
            {
                x[cur++]=*it;
                int s=*it;
                it++;
                val.erase(s);
            }
        }
        for(int i=1;i<=n-1;i++)
            printf("%d ",x[i]);
        printf("%d\n",x[n]);
    }
    return 0;
}

1007  Chiaki Sequence Revisited 数学题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
#include <bits/stdc++.h>
#define mst(a,b) memset(a,b,sizeof(a))
#define ALL(x) x.begin(),x.end()
#define pii pair<int,int>
#define eps 1e-4
inline long long lowbit(long long x){return x&-x;}
const int N = 1e6+10;
const long long mod = (long long)1e9+7;
const int INF=0x3f3f3f3f;
const long long LINF=(1LL<<62);
typedef long long LL;
typedef unsigned long long ULL;
//#define LOCAL
const double PI = acos(-1.0);
using namespace std;

LL n,inv2,p[63];

LL q_pow(LL base, LL b){
  LL res = 1;
  while(b){
    if(b&1) res = res*base%mod;
    base = base*base%mod;
    b>>=1;
  }
  return res;
}
bool check(LL x){   //为什么要这么写呢，看上面打的表，除以每个2^i就可以得出2^i有多少个，这样子加完就得到对应的a[x]是多少。
  LL temp = 0;
  for(int i = 0; i <= 62; i++){
    temp += x/p[i];
    if(temp >= n-1) return true;
  }
  return temp >= n-1;
}
LL cal(LL x){
  LL temp = 0;
  for(int i = 0; i <= 62; i++) temp += x/p[i];
  return temp;
}
int main(){
#ifdef LOCAL
    freopen("out.txt", "w", stdout);
#endif // LOCAL
    inv2 = q_pow(2,mod-2);  //2的逆元，等下等差数列求和的时候要用
    p[0] = 1;
    for(int i = 1; i <= 62; i++) p[i] = p[i-1]*2; //预处理2^i
    int T; scanf("%d",&T);
    while(T--){
      scanf("%lld",&n);
      if(n==1){
        printf("1\n");
        continue;
      }
      LL l = max(1LL,n/2-30), r = min(n,n/2+30), mid, pos;
      while(l<=r){
        mid = (l+r)>>1;
        if(check(mid)){   //二分找n对应的a[n]；
          pos = mid;      //pos即为a[n]
          r = mid-1;
        }else l = mid+1;
      }
      LL res = pos-1, now = 0;  //这里pos-1是因为在a[n]位置的n可能不是刚好符合2^i，所以要找前面一个，前面一个必定是符合2^i个的。
      for(int i = 0; i <= 62; i++){
        if(p[i]>res) break;
        LL temp = res/p[i];
        temp %= mod;
        now = (now+p[i]%mod*(temp+1)%mod*temp%mod*inv2%mod)%mod;  //等差数列求和，不要忘记Mod
      }
      now = (now+(n-1-cal(res)%mod)%mod*pos%mod)%mod;  //剩下这里就是那些不完整的a[n]了
      printf("%lld\n",(1+now)%mod);
    }
    return 0;
}

1011 Time Zone 水。

7.25 [ 多校2](http://acm.hdu.edu.cn/contests/contest_show.php?cid=803)

1003 Cover 没看题，听了题解，大概是给你一个无向图，让你求至少要多少一笔画才能把它画完。一笔画有两种情况，一种是欧拉路，一种是欧拉回路，也就是说，对于图中的所有点，度数为奇数的要么是0（回路），要么是2（一个进来的点，一个出去的点）。所以要把一个图构造成欧拉路/回路的话，就意味着要在图中x个奇数度的点中连接x/2条边，然后在对于新生成的图，找欧拉路，然后再把添上去的x/2条边删去，分成的几条路就是一笔画的结果。

1004  Game 水题，先手必赢。先手可以取或者不取1。

1005  Hack It 不知所措的构造题。要求是构造出一个n*n(n<=2000)的矩阵，你可以在里面填黑点，但是你不能让任意四个黑点组成一个矩形（四个角），要求是至少包含85000个黑点。老实说，我无法理解构造方法。

1007 Naive Operations 线段树 题解

1010 Swaps and Inversions 水题。数逆序数对，再乘以min(x,y)即可。这里我发现逆序数对数有x个，就可以通过交换相邻数字x次使得它不存在逆序数。

用归并排序可以得到逆序数对个数。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm>
#define MOD 1000000007
using namespace std;
typedef long long ll;
long long sum;
int a[500005];
int temp[500005];
void sort2(int a[],int l,int mid,int r)
{
    int i=l,j=mid+1,k=0;
    while(i<=mid&&j<=r)
    {
        if(a[i]<=a[j])
        {
            temp[k++]=a[i++];
        }
        else
        {
            temp[k++]=a[j++];
            sum+=mid-i+1;
        }
    }
    while(i<=mid)  temp[k++]=a[i++];
    while(j<=r)    temp[k++]=a[j++];

    for(int i=l,k=0; i<=r; k++,i++)
        a[i]=temp[k];
}

void sort1(int a[],int l,int r)
{
    int mid;
    if(l<r)
    {
        mid=(l+r)/2;
        sort1(a,l,mid);
        sort1(a,mid+1,r);
        sort2(a,l,mid,r);
    }
}
int main()
{
    int n;
    long long x,y;
    while(scanf("%d%lld%lld",&n,&x,&y)!=EOF)
    {
        sum=0;
        for(int i=0; i<n; i++)
            scanf("%d",&a[i]);
        sort1(a,0,n-1);
        printf("%lld\n",sum*min(x,y));
    }
    return 0;
}

7.24 [ The 2018 ACM-ICPC China JiangSu Prov..](https://www.jisuanke.com/contest/1408)

A. Plague Inc 水题暴力，遍历每个点到感染源的路求最远。

B. Array n个数，k对逆序数，求可能的方案数。这是一道DP 。

D.  Persona5 公式题

E.  Massage 公式结论题

I. T-shirt ////////////////////////////////////

J. Set 结论是(n+1)!-1，用java写

K.  Road 连通图，删去尽可能多的路，使得每个城市到第0号城市的最短路长度不变，求可能的方案数量。

用floyd先求出每个城市之间的最短路，然后对每条0i城市的最短路，判断0j城市的距离加上i到j的原始距离是否还和最短路相等，相等的话，在j城市上的最短路径+1。最后将他们乘起来。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
#include <bits/stdc++.h>
using namespace std;
const int INF=0x3f3f3f3f;
const int maxn=350;
const long long MOD=1e9+7;
int dist[maxn],g[maxn][maxn],f[maxn][maxn],N;
long long road[maxn];
long long floyd()
{
    long long ans=1;
    memset(road,0,sizeof(road));

    for (int k=0;k<N;k++)
        for (int i=0;i<N;i++)
            for (int j=0;j<N;j++)
                if (i!=k&&i!=j&&j!=k)
                    g[i][j]=min(g[i][j],g[i][k]+g[k][j]);
    g[0][0]=0;
    for(int i=0;i<N;i++)
        for(int j=0;j<N;j++)
        if(i!=j&&g[0][i]+f[i][j]==g[0][j])
    {
        road[j]++;
    }
    for(int i=1;i<N;i++)
        if(road[i])
            ans=(ans*road[i])%MOD;
    return ans;

int main()
{
    while(scanf("%d",&N)!=EOF)
    {
        memset(g,INF,sizeof(g));
        string s;
        for(int i=0;i<N;i++)
        {
            cin>>s;
            for(int j=0;j<s.size();j++)
            {
                if(s[j]=='0')
                    f[i][j]=g[i][j]=INF;
                else
                	f[i][j]=g[i][j]=s[j]-'0';
            }
        }
        printf("%lld\n",floyd());
    }
    return 0;
}

7.26 [ Nordic Collegiate Programming Contes...](https://www.jisuanke.com/contest/1410)

A. Adjoin the Networks 回头补把。

B. Bell Ringing 用生成全排列的邻位互换法：（具体方法解释可以看排列组合的文章）

仔细想想不就是把n插入到已完成的n-1阶排列的不同位置中得到n阶排列吗？

n=1; 1

n=2; 12 , 21

n=3; 123, 132, 312, 321, 231, 213

……

用这种方法可以产生出任意n阶全排列，（而且符合bellring中的移动规律，即每个数移动的位置最多为1，就能一下子构造出n！个不重复的全排列）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
#include <bits/stdc++.h>
using namespace std;
int n;
int A[15];
int dir[15];

void print()
{
    for(int i=1;i<n;i++)
        printf("%d ",A[i]);
    printf("%d\n",A[n]);
}
bool IF_Active(int i) //判断是否活跃（前面的数字比它小就是活跃）
{
    if(i+dir[i]<=0||i+dir[i]>n)
        return false;
    if(A[i+dir[i]]<A[i])
        return true;
    return false;
}

int MAX_Active() //找到最大的活跃数字
{
    int id=n+1;
    for(int i=1;i<=n;i++)
    {
        if(IF_Active(i)&&A[id]<A[i])
            id=i;
    }
    return id;
}
int Swap(int i) //交换最大的活跃数字和它前面的那个数字，注意方向也要交换
{
    int c=A[i];
    A[i]=A[i+dir[i]];
    A[i+dir[i]]=c;

    c=dir[i];
    dir[i]=dir[i+c];
    dir[i+c]=c;

    return i+c;
}
void UPdate(int index)
{
    for(int i=1;i<=n;i++)
    {
        if(A[index]<A[i])
            dir[i]=-dir[i];
    }
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        A[i]=i;
        dir[i]=-1;
    }
    print();
    
    while(1)
    {
        int id=MAX_Active();
        if(id==n+1) break;
        id=Swap(id);
        UPdate(id);
        print();
    }
    return 0;
}

C. Cryptographer’s Conundrum 水

D. Disastrous Downtime 水，取最大的ai~ai+1000范围内的数字个数即可。

E.Entertainment Box n个节目，k个录像带，给出每个节目的播放时间，求最多能录几个节目。

用multiset维护当前正在录制的所有节目的结束时间，二分找到最接近下一个要录的节目的起始时间且小于起始时间的录像带，把这个录像带中的r替换成下一个要录的节目，cnt++，如果没有找到并且集合的size还不到k个的话，就直接把r放进去，cnt++。最后输出cnt。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
const int N=1e5+10;
struct node
{
    int l,r;
} nn[N];
bool cmp(node a,node b)
{
    if(a.r==b.r)
        return a.l<b.l;
    return a.r<b.r;
}

multiset<int>q;
multiset<int>::iterator pos;
int main()
{
    int n,k;
    int cnt=0;
    int i;
    scanf("%d%d",&n,&k);
    for(int i=0; i<n; i++)
        scanf("%d%d",&nn[i].l,&nn[i].r);
    sort(nn,nn+n,cmp);
    for(i=0; i<n; i++)
    {
        if(q.empty())
        {
            cnt++;q.insert(nn[i].r);
            continue;
        }
        if(*q.begin()>nn[i].l)
        {
            if(q.size()<k)
            {
                cnt++;q.insert(nn[i].r);
            }
            continue;
        }
        pos=q.upper_bound(nn[i].l);
        pos--;
        if(*pos<=nn[i].l)
        {
            cnt++;
            q.erase(pos);
            q.insert(nn[i].r);
        }
        else
        {
            if(q.size()<k)
            {
                cnt++;q.insert(nn[i].r);
            }
        }
    }
    printf("%d\n",cnt);
    return 0;
}

G.Goblin Garden Guards 给n个哥布林的位置（x，y），给出m个圆，对于每一个圆，输出最大的不在圆内的哥布林数目。

由于哥布林的位置是整数，那么对于圆，可以预处理出距离圆心0~r范围内的x最大偏差值和y的最大偏差值，如果哥布林的x，y与圆心的偏差值有一者在最大偏差值之外，就cnt++。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#include <iostream>
#include <algorithm>
#define MOD 1000000007
using namespace std;
typedef long long ll;
struct point
{
    int x,y;
}p[100010];
bool cmp(point a,point b)
{
    return a.y<b.y;
}
vector<int>v[100010];
vector<int>d[110];
void init()
{
    for(int r=1;r<=100;r++)
        for(int i=0;i<=r;i++)
            d[r].push_back((int)floor(sqrt(1.0*r*r-i*i)));
}
int main()
{
    init();
    int g,m,x,y,r;
    scanf("%d",&g);
    for(int i=0;i<g;i++)
        scanf("%d%d",&p[i].x,&p[i].y);
    sort(p,p+g,cmp);
    for(int i=0;i<g;i++)
        v[p[i].x].push_back(p[i].y);
    scanf("%d",&m);
    int ans=0;
    for(int i=0;i<m;i++)
    {
        scanf("%d%d%d",&x,&y,&r);
        int left=max(0,x-r),right=min(10000,x+r);
        for(int dd=left;dd<=right;dd++)//横坐标
        {       
            int c=abs(dd-x);
            int yl=max(0,y-d[r][c]),yr=min(10000,y+d[r][c]);
            int pos1=lower_bound(v[dd].begin(),v[dd].end(),yl)-v[dd].begin();
            int pos2=upper_bound(v[dd].begin(),v[dd].end(),yr)-v[dd].begin();
            v[dd].erase(v[dd].begin()+pos1,v[dd].begin()+pos2);
            ans+=pos2-pos1;
        }
    }
    printf("%d\n",g-ans);
    return 0;
}

7.28 teemo场

A. Teemo’s bad day 裸的并查集，判断两个数字的根是否一样，不一样就cnt++，顺便union即可。（好久没写并查集find都写炸）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
#include <bits/stdc++.h>
using namespace std;
int a[500010],b[500010];
int fa[100010];
int Find(int x)
{
    if(fa[x]==x)return x;
    return fa[x]=Find(fa[x]);
}
void Union(int p,int q)
{
    int rp=Find(p),rq=Find(q);
    if(rp!=rq)
        fa[rp]=rq;
}
void init(int n)
{
    for(int i=0;i<100010;i++)
        fa[i]=i;
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n,cnt=0;
        scanf("%d",&n);
        init(n);
        for(int i=0;i<n;i++)
            scanf("%d",&a[i]);
        for(int i=0;i<n;i++)
        {
            scanf("%d",&b[i]);
            if(a[i]==b[i]) continue;
            if(Find(a[i])!=Find(b[i]))
            {
                cnt++;Union(a[i],b[i]);
            }
        }
        printf("%d\n",cnt);
    }
    return 0;
}

B. Teemo’s hard problem 题目意思是给你一个数列，你可以任意反转[L,R]，使得这个数列的非递减序列最长。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
#include <bits/stdc++.h>
#define INF 0x3f3f3f3f3f3f3f3f
#define MOD 1000000007
using namespace std;
typedef long long ll;
int a[2010];
int pre[2010];//1的前缀长度（包括自己）
int suf[2010];//2的后缀长度（包括自己）
int dp[2005][2005][4];//[i,j]中以k结尾的最长非递增序列长度
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n;
        scanf("%d",&n);
        memset(pre,0,sizeof(pre));
        memset(suf,0,sizeof(suf));
        memset(dp,0,sizeof(dp));
        for(int i=1; i<=n; i++)
        {
            scanf("%d",&a[i]);
            if(a[i]==1)pre[i]=pre[i-1]+1;
            else pre[i]=pre[i-1];
        }
        for(int i=n; i>=1; i--)
        {
            if(a[i]==2)suf[i]=suf[i+1]+1;
            else suf[i]=suf[i+1];
        }
        for(int i=1; i<=n; i++)
        {
            dp[i][i][a[i]]=1;
            for(int j=i+1; j<=n; j++)
            {
                if(a[j]==1)
                {
                    dp[i][j][1]=max(dp[i][j-1][1],dp[i][j-1][2])+1;
                    dp[i][j][2]=dp[i][j-1][2];
                }
                else if(a[j]==2)
                {
                    dp[i][j][1]=dp[i][j-1][1];
                    dp[i][j][2]=dp[i][j-1][2]+1;
                }
            }
        }
        int ans=0;
        for(int i=1; i<=n; i++)
            for(int j=i; j<=n; j++)
            {
                ans=max(ans,pre[i-1]+max(dp[i][j][1],dp[i][j][2])+suf[j+1]);
            }
        printf("%d\n",ans);
    }
    return 0;
}

C. Teemo’s tree problem 又是一个dp

F. Teemo’s dream 没看题

G .Teemo’s convex polygon 将多边形对角线相连，其对角线最多被分割成多少段？
$$
max=(n^4-6n^3+17n^2-24*n)/12
$$
J. Teemo’s formula 结论是$Σ_{k=1}^nk^2C_n^k=2^{n-2}n(n+1)$

K.Teemo’s reunited 求的是其他所有的点到某一点的距离和的最小值，就是曼哈顿距离。HDU 4311Meeting point-1

这题也是用“分治”，虽说题目要求的是曼哈顿距离，但是我们为什么真的就要一步到位的求呢，可以横纵坐标分开求，先x排序，然后遍历一遍，求出横坐标的距离，然后y排序，遍历一遍求出坐标的距离加在刚才求得的x的距离上，就是曼哈顿距离了。

这里有一个非常巧妙但是其实很显而易见的东西：假定现在我们已经按x排好序了分别是ABC三个点，那么C到AB的距离和是|C-A|+|C-B|，又因为已经排序了，那么绝对值可以去掉，得(C-A)+(C-B)，那么就是2*C-(A+B)，也就是说一个点到它前面的点的距离的和等于它前面的点的个数乘以它的自己再减去前面所有点的和，到这里你是不是想到求一个数列的和的时候我们遍历一遍数列就得到了，通过这个方法我们用O(n)就得到了一个点到它前面的点的距离和，然后再倒着遍历一遍数列用相似的思想把它到它后面的点的距离再加上就行了。

还有一种也是分开x,y排序求和，不过可以这么做：先直接求出最前面的点到所有点的距离，然后依次遍历数列，通过后面一个点跟前面一个点的关系，找出差值相减，就是了。不明白的话仔细想想或者画图看看。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
#include<iostream>
#include<cstring>
#include<algorithm>
#define INF 1000000000000007
using namespace std;
struct node{
	long long x,y;
	long long sum;
}a[100005];
bool cmp1(node a,node b)
{
	return a.x<b.x;
}
bool cmp2(node a,node b)
{
	return a.y<b.y;
}
int main(){
	int t,n;
	scanf("%d",&n);
	long long ans=INF;
	memset(a,0,sizeof(0));
	for(int i=0;i<n;i++)  
        scanf("%lld%lld",&a[i].x,&a[i].y);
	sort(a,a+n,cmp1);
	long long sum=0;
	for(int i=0;i<n;i++)
    {
		a[i].sum=i*a[i].x-sum;
		sum+=a[i].x;
	}
	sum=0;
	for(int i=n-1;i>=0;i--)
    {
		a[i].sum+=sum-(n-1-i)*a[i].x;
		sum+=a[i].x;
	}
	sort(a,a+n,cmp2);
	sum=0;
	for(int i=0;i<n;i++)
    {
		a[i].sum+=i*a[i].y-sum;
		sum+=a[i].y;
	}
	sum=0;
	for(int i=n-1;i>=0;i--)
    {
		a[i].sum+=sum-(n-1-i)*a[i].y;			
		sum+=a[i].y;
		ans=min(ans,a[i].sum);
	}
	printf("%lld\n",ans);
    return 0;
}

7.29

A.  Coins 概率dp….不懂不懂

B. The Difference 水题

D. Fence Building 一个圆，一个圆的内接n边形，连接多边形对角线，求整个圆被分割成几块。

OEIS大法好。。。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
#include<stdio.h>
#include<iostream>
#include<string.h>
#include<math.h>
#include<time.h>
#include<stdlib.h>
#include<queue>
#include<stack>
#include<set>
#include<map>
#include<vector>
#include<cassert>
#include<algorithm>
#define INF 0x3f3f3f3f3f3f3f3f
#define MOD 1000000007
#define MAXN 10000000
using namespace std;
typedef long long ll;
void extgcd(ll a,ll b,ll d,ll &x,ll &y)   //a,b都为正整数
{
    if(b==0){d=a;x=1;y=0;}
    else{extgcd(b,a%b,d,y,x);y=y-x*(a/b);}
}
ll inverse(ll a,ll p)
{
    ll d,x,y;
    extgcd(a,p,d,x,y);
    return (x%p+p)%p;
}
int main()
{
    int t;
    ll n;
    scanf("%d",&t);
    for(int cs=1;cs<=t;cs++)
    {
        scanf("%lld",&n);
        n%=MOD;
        ll temp1=n,temp2=(temp1*n)%MOD,temp3=(temp2*n)%MOD,temp4=(temp3*n)%MOD;
        temp1=(temp1*18ll)%MOD,temp2=(temp2*23ll)%MOD,temp3=(temp3*6ll)%MOD;
        ll temp=inverse(24ll,MOD);
        //printf("%lld %lld %lld %lld %lld\n",temp1,temp2,temp3,temp4,temp);
        ll fz=(temp4-temp3+MOD)%MOD;
        fz=(fz+temp2)%MOD;
        fz=(fz-temp1+24+MOD)%MOD;
        ll ans=(fz*temp)%MOD;
        printf("Case #%d: %lld\n",cs,ans);
    }
    return 0;
}

G.The Mountain 水

I. A Possible Tree 给你一棵树，q个询问，问的是x->y路径上的异或和为val , 问你最多有几个询问是真的？

带权并查集。由于异或的特点，假设某个点为根，比如0，那么比如2->5的异或值，就是2->1的异或值和5->1的异或值异或一下。所以我们用yihuo[i]来表示i到源点的异或和。如果两个数的源点已经一样，那么判断一下val==yihuo[i]^yihuo[j]即可，若是不一样，就把他们union，同时yihuo[rootp]=yihuo[p]^yihuo[q]^val。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
#include <bits/stdc++.h>
using namespace std;
int fa[100010],yihuo[100010];
int Find(int x)
{
    if(x!=fa[x])
    {
        int tmp=fa[x];
        fa[x]=Find(fa[x]);
        yihuo[x]^=yihuo[tmp];
        return fa[x];
    }
    return x;
}

bool Union(int p,int q,int val)
{
    int rp=Find(p),rq=Find(q);
    if(rp!=rq)
    {
        fa[rp]=rq;
        yihuo[rp]=yihuo[p]^yihuo[q]^val;
        return true;
    }
    if((yihuo[p]^yihuo[q])!=val)
        return false;
    return true;
}
void init(int n)
{
    for(int i=1;i<=n;i++)
    {
        fa[i]=i;yihuo[i]=0;
    }
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        int n,k,u,v,val;
        scanf("%d%d",&n,&k);
        init(n);
        for(int i=0;i<n-1;i++)
            scanf("%d%d",&u,&v);
        int flag=1,ans=0;
        for(int i=0;i<k;i++)
        {
            scanf("%d%d%d",&u,&v,&val);
            if(!Union(u,v,val)&&flag)
            {
                flag=0;
                ans=i;
            }
        }
        printf("%d\n",ans);
    }
    return 0;
}

K.  Sum of the Line 给你一个n，分析之后发现求的是所有gcd(n,i)=1（i<=n）的数的平方和。

用容斥，先用公式$\frac{n(n+1)(2n+1)}{6}$求出1~n的平方和，然后筛出sqrt(n)内的素数，并求出n的所有质因数，然后对于质因数的乘积tot，如果质因数的个数是奇数，就加上$tot^2*(1^2+2^2+3^2……+(n/tot)^2)$，是偶数就减去。

或者用莫比乌斯反演来做

（补莫比乌斯反演做法）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
#include<bits/stdc++.h>
#define INF 0x3f3f3f3f3f3f3f3f
#define MOD 998244353
#define MAXN 10000
using namespace std;
typedef long long ll;
ll pri[10010],num=0;
bool vis[10010];
vector<ll>pr;
void init()
{
    ll i,j;
    for(i=2;i<MAXN;i++)
    {
        if(vis[i]==false)pri[num++]=i;
        for(j=0;j<num&&i*pri[j]<MAXN&&i%pri[j]!=0;j++)
            vis[i*pri[j]]=true;
    }
}
void extgcd(ll a,ll b,ll d,ll &x,ll &y)
{
    if(b==0){d=a;x=1;y=0;}
    else{extgcd(b,a%b,d,y,x);y=y-x*(a/b);}
}
ll inverse(ll a,ll p)
{
    ll d,x,y;
    extgcd(a,p,d,x,y);
    return (x%p+p)%p;
}
int main()
{
    init();
    int t;
    ll n;
    scanf("%d",&t);
    while(t--)
    {
        scanf("%lld",&n);
        pr.clear();
        ll xs=inverse(6ll,MOD);
        ll tot=(((n*(n+1))%MOD*(2*n+1))%MOD*xs)%MOD;
        ll temp=n;
        for(int i=0;i<num;i++)
        {
            if(temp%pri[i]==0)
            {
                pr.push_back(pri[i]);
                while(temp%pri[i]==0)
                    temp/=pri[i];
            }
        }
        if(temp>1)pr.push_back(temp);
        int len=pr.size();
        ll ans=0;
        for(int i=1;i<(1<<len);i++)
        {
            int cnt=0;//有几个1
            ll d=1;
            for(int j=0;j<len;j++)
            {
                int temp=i>>j&1;
                if(temp==1)
                {
                    cnt++;d=d*pr[j];
                }
            }
            ll gs=n/d;
            ll g=(((gs*(gs+1))%MOD*(2*gs+1))%MOD*xs)%MOD;
            if(cnt%2==0)ans=(ans-((d*d)%MOD*g)%MOD+MOD)%MOD;
            else ans=(ans+((d*d)%MOD*g))%MOD;
            }
        }
        printf("%lld\n",(tot-ans+MOD)%MOD);
    }
    return 0;
}

7.30 多校三

A.  Problem A. Ascending Rating 输入n,m,k,p,q,r,MOD,表示一个长度为n的数列，给你前k个数字，（后面的要根据递推式自己写），然后m表示一个[l,l+m]的区间，从l=1开始，在这个区间中有两个值，一个是MAX，一个是CNT，起始都为0，从区间的第一个数开始扫，如果扫到的数字比MAX大，让MAX=ai，并且CNT++。求的是$A =\sum_{i=1}^{n-m+1}{MAX_i 异或i}$ , $B=\sum_{i=1}^{n-m+1}{CNT_i 异或i}$

思路是用一个单调队列从最后一个区间往前倒着维护，如果队列为空，则直接放入ai，若ai>=队首元素，则将队列中的元素全部弹出，同时将ai放入，若ai小于队首元素，则将队尾中小于ai的元素弹出，将ai放入队尾中，每一个区间的cnt值即为队列中元素的个数，而MAX值则为队首元素。如果队首元素的位置不在下一个区间范围内，则弹出。注意STL的双端队列会被卡，这里可以用数组直接模拟。（可以补一个正向写的，但是我WA到死，主要就是用单调栈来维护每一个数字右边的第一个比他大的位置，最后一个栈里的数的stack设为n+1，然后从右到左，dp[n-1]=1，dp[i]=dp[stack[i]]+1，………然后单调队列维护区间最大值）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include <bits/stdc++.h>
using namespace std;
long long a[10000010];
long long que[20000010];
int main()
{
    int t,n,m,k,p,q,r,MOD;
    int size,front,rear;
    scanf("%d",&t);
    while(t--)
    {
        size=0;
        front=rear=1e7+5;
        scanf("%d%d%d%d%d%d%d",&n,&m,&k,&p,&q,&r,&MOD);
        for(int i=1;i<=k;i++)
            scanf("%lld",&a[i]);
        for(int i=k+1;i<=n;i++)
            a[i]=(1LL*p*a[i-1]+1LL*q*i+r)%MOD;
        long long MAX=0,CNT=0;
        for(int i=n;i>=1;i--)
        {
            if(size==0)
            {
                que[front]=i;size=1;
            }
            else
            {
                if(a[que[front]]<=a[i])
                {
                    front=rear=1e7+5;
                    que[front]=i;
                    size=1;
                }
                else
                {
                    while(size>0&&a[que[rear]]<=a[i])
                        size--,rear--;
                    que[rear+1]=i;rear++;
                    size++;
                }
            }
            if(i<=n-m+1)
            {
                MAX+=a[que[front]]^i;
                CNT+=size^i;
                while(que[front]>=(i+m-1))
                    front++,size--;
            }
        }
        printf("%lld %lld\n",MAX,CNT);
    }
    return 0;
}

C.  Problem C. Dynamic Graph Matching 在一个图中，任意k条不共点的边可以构成一个匹配。给你n个点，有q个操作，操作分两种，一种是+ u v，在u v中间连线，一个是- u v，删边，两点之间可以连多条路线。问你对于每一次操作，k=1,2，…… n/2的匹配方案分别有多少？

思路：树状DP。（补）

D. Problem D. Euler Function 水。求φ(n)为合数的第k个数。根据规律可看到，从第7个开始就都是偶数。

F. Problem F. Grab The Tree 水。很容易看出sum=0时平手，否则就是先手赢。

L. Problem L. Visual Cube 水。直接写。

7.31 ACM-ICPC 2015 Shenyang Preliminary C…

B.  Best Solver （补）

C. Minimum Cut （补）

F.  Fang Fang 水。

J.  Jesus Is Here 有、搞的题。把递推关系算出来……表示不想再写一编代码，就那个意思反正。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
#include<bits/stdc++.h>
using namespace std;
#define MOD 530600414
typedef long long ll;
ll sum[210000];
ll num[210000];
ll pre[210000],suf[210000],ans[210000];
void init()
{
    sum[1]=5;sum[2]=8;num[1]=1;num[2]=2;
    for(int i=3;i<=201314;i++)
    {
        sum[i]=(sum[i-1]+sum[i-2])%MOD;
        num[i]=(num[i-1]+num[i-2]+1)%MOD;
        if(i%2==1)sum[i]=(sum[i]+5)%MOD;
        else sum[i]=(sum[i]+3)%MOD;
    }
    pre[1]=5;pre[2]=11;suf[1]=5;suf[2]=13;
    for(int i=3;i<=201314;i++)
    {
        ll x;
        if(i%2==1)x=5;else x=3;
        pre[i]=((((num[i-1]+1)*(sum[i-2]+x))%MOD+pre[i-2])%MOD+pre[i-1])%MOD;
        suf[i]=((((num[i-2]+1)*(sum[i-1]+x))%MOD+suf[i-2])%MOD+suf[i-1])%MOD;
    }
    ans[1]=5;ans[2]=16;
    for(int i=3;i<=201314;i++)
    {
        ll x;
        if(i%2==1)x=5;else x=3;
        ll temp1=((num[i-1]+1)*suf[i-2])%MOD;
        ll temp2=((num[i-2]+1)*pre[i-1])%MOD;
        ll temp3=(((num[i-1]+1)*(num[i-2]+1))%MOD*x)%MOD;
        ans[i]=((((temp1+temp2)%MOD+temp3)%MOD+ans[i-2])%MOD+ans[i-1])%MOD;
    }
}
int main()
{
    init();
    int t,n;
    scanf("%d",&t);
    for(int kase=1;kase<=t;kase++)
    {
        scanf("%d",&n);
        if(n<5)printf("0\n");
        else
        {
            n-=4;
            printf("Case #%d: %lld\n",kase,ans[n]);
        }
    }
    return 0;
}

M.  Largest Point 写的我脑子有点不清楚了……

8.1多校4

B. Harvest of Apples 题意是从n个苹果里面选取最多m个苹果的方案数量。m、n、t<=1e5

思路：莫队分块+组合预处理，原来莫队中的区间[l,r]在这里用n、m代替了。

接下来是推公式部分：

S(n,m)表示$\sum_{i=1}^n\sum_{j=1}^mC_i^j$

我们可以得出$S(n,m)=S(n,m-1)+C_n^m$ ,——-①

又因为有$C_n^m=C_{n-1}^m+C_{n-1}^{m-1}$（组合数学的一个基本公式），因此又可以推出：$S(n,m)=S(n-1,m)+S(n-1,m-1)=2S(n-1,m)-C_{n-1}^m$——–②

有了①②两个式子，我们就可以得到S(n,m)和S(n-1,m)、S(n+1,m)、S(n,m-1)、S(n,m+1)之间的关系，先预处理出n！和相应的需要的逆元，然后把输入的查询分块，按照代码中所示的“套路”排序法，排一排，然后对于每个n，m开始处理，分四种情况这样。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
const long long MOD =1e9+7;
typedef long long ll;
ll multi[N];
ll devide[N];
ll ans[N];
ll pos[N];
ll er;
int D=(int)sqrt(1.0*N);
struct node{
    int n,m;
    int id;
    bool operator <(const node& p) const{
        if(pos[n]==pos[p.n]) return m<p.m;
        return n<p.n;                           //N大的排前面
    }
};
node qujian[N];
ll ex_gcd(ll a,ll b,ll &x,ll &y)//扩展欧几里得（扩展gcd）
{
	if (a==0&&b==0) return -1;
	if (b==0){x=1;y=0;return a;}
	ll d=ex_gcd(b,a%b,y,x);
	y-=a/b*x;
	return d;
}

ll mod_inverse(ll a,ll n)//乘法逆元,n取模
{
	ll x,y;
	ll d = ex_gcd(a,n,x,y);
	return (x%n+n)%n;
}

void init(int n)
{
    multi[0]=1;
    multi[1]=1;
    for(int i=2;i<=n;i++)
        multi[i]=multi[i-1]*i%MOD;
    devide[n]=mod_inverse(multi[n],MOD);
    for(int i=n-1;i>=0;i--)
        devide[i]=devide[i+1]*(i+1)%MOD;
}
ll cal(int n,int m)
{
    return ((multi[n]*devide[m])%MOD*devide[n-m])%MOD;
}
void operation1(int n,int m,ll &res)
{
    res=((2ll*res)%MOD-cal(n,m)%MOD+MOD)%MOD;
}
void operation2(int n,int m,ll &res)
{
    res=(res+cal(n-1,m))%MOD*er%MOD;
}
void operation3(int n,int m,ll &res)
{
    res=(res+cal(n,m+1))%MOD;
}
void operation4(int n,int m,ll &res)
{
    res=(res-cal(n,m)+MOD)%MOD;
}
int main()
{
    init(100000);
    int t;
    int n,m;
    er=mod_inverse(2ll,MOD);
    scanf("%d",&t);
    for(int i=1;i<=t;i++)
    {
        scanf("%d%d",&qujian[i].n,&qujian[i].m);
        qujian[i].id=i;
        pos[i]=i/D;
    }
    sort(qujian+1,qujian+t+1);
    int curl,curr;
    curl=curr=1;
    ll res=2;
    for(int j=1;j<=t;j++)
    {
        while(curl<qujian[j].n) operation1(curl++,curr,res);
        while(curr<qujian[j].m) operation3(curl,curr++,res);
        while(curl>qujian[j].n) operation2(curl--,curr,res);
        while(curr>qujian[j].m) operation4(curl,curr--,res);
        ans[qujian[j].id]=res;
    }
    for(int i=1;i<=t;i++)
        printf("%lld\n",ans[i]);
    return 0;
}

D. Nothing is Impossible 水，按占比来算就好。

E. Matrix from Arrays 讲一下思想吧，再写一边代码的话可能又要写一万年。对于这个块的计算，比如这个块的四个角顺时针分别叫：a,b,c,d，将(0,0)点到(i,j)点的里面所有的数字和叫做pre，那么就是pre[b]-pre[b]-pre[d]+pre[a]。分析一下就可以得到，对于所有的无限大的矩阵，他都是重复某个特定的矩阵来的。这些矩阵有以下长度规律：（L为给定数组的长度，L从1~10，）

len[1]=1,len[2]=4,len[3]=3,len[4]=8,len[5]=10,len[6]=12,len[7]=14,len[8]=16,len[9]=18,len[10]=20。

矩阵为n*n。

故对于给定的L和数组可以先处理出重复矩阵的样子，然后再进行分块和的计算。

关于分块和的计算（pre），把块内完整的小矩阵的个数算出来求个和，除了完整的还有不完整的，不完整的其实也好看，就是矩阵最左边和最上面的部分，也用pre算出来就行。

J. Let Sudoku Rotate 数独，有一个16*16的数独 数独内的数字从0~E，一开始数独是完美的，可是有个人逆时针旋转了数独中的某几块（4x4），导致数独不完美了，给你这个旋转后的数独，要求还原他至少要再旋转几步？

dfs+剪枝。

写出下列几个操作：

  1. 顺时针旋转4*4的方块；
  2. 判断每行的总和是否都为120；
  3. 判断每行和每列的元素是否都不重复；
  4. dfs，由于一行块有4个分块，因此四重循环，同一个x分别对应y的起始：0，4，8，12，循环+1表示旋转次数+1，如果在2、3的判断中都满足这写要求，说明可以进行下一个x+4（起始行）块的旋转操作dfs，step+本次旋转的操作（i，j，k，l四重循环），要是不满足还是要继续。当x==16或者是step比当前已知的最小ans要大的时候都可以return。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
#include <bits/stdc++.h>
using namespace std;
const int N = 100010;
const int INF = 0x3f3f3f3f;
const long long MOD =1e9+7;
typedef long long ll;
char m[20][20];
char cop[4][4];
int ans=64;
void print()
{
    printf("\n");
    for(int i=0;i<16;i++,printf("\n"))
        for(int j=0;j<16;j++)
            printf("%c",m[i][j]);
    printf("\n");
}
int rol(int x,int y)
{
    for(int i=0;i<4;i++)
        for(int j=0;j<4;j++)
            cop[i][j]=m[x+3-j][y+i];
    for(int i=0;i<4;i++)
        for(int j=0;j<4;j++)
            m[i+x][j+y]=cop[i][j];
}
bool sum(int x)
{
    for(int j=x;j<x+4;j++)
    {
        int temp=0;
        for(int i=0;i<16;i++)
        {
            temp=temp+((m[x][i]>='0'&&m[x][i]<='9')?(m[x][i]-'0'):(m[x][i]-'A'+10));
        }
        if(temp!=120) return false;
    }
    return true;
}
bool multi(int x)
{
    int vis[16]={0};
    for(int j=x;j<x+4;j++)
    {
        memset(vis,0,sizeof(vis));
        for(int i=0;i<16;i++)
        {
            int temp=((m[j][i]>='0'&&m[j][i]<='9')?(m[j][i]-'0'):(m[j][i]-'A'+10));
            vis[temp]++;
            if(vis[temp]>1) return false;
        }
    }

    for(int i=0;i<16;i++)
    {
        memset(vis,0,sizeof(vis));
        for(int j=0;j<=x+3;j++)
        {
            int temp=((m[j][i]>='0'&&m[j][i]<='9')?(m[j][i]-'0'):(m[j][i]-'A'+10));
            vis[temp]++;
            if(vis[temp]>1) return false;
        }
    }
    return true;
}
void dfs(int x,int step)
{
    if(step>ans) return;
    if(x==16)
    {
        ans=min(ans,step);return;
    }
    for(int i=0;i<4;i++,rol(x,0))
    for(int j=0;j<4;j++,rol(x,4))
    for(int k=0;k<4;k++,rol(x,8))
    for(int l=0;l<4;l++,rol(x,12))
    {
        if(!(sum(x)&&multi(x))) continue;
        dfs(x+4,step+i+j+k+l);
    }
}
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        getchar();
        for(int i=0;i<16;i++)
            scanf("%s",m[i]);
        ans=64;
        dfs(0,0);
        printf("%d\n",ans);
    }
    return 0;
}

K. Expression in Memories 表达式中有一些是用？代替的，问你这个表达式能否符合正确的要求，能的话输出任意成立的表达式（不含？）。注意细节，一开始对“+0?”单独扫，？填运算符号。完了之后就按顺序扫，判断是否符合。（注意细节，容易wa）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
#include <bits/stdc++.h>
using namespace std;
int main()
{
    int t;
    scanf("%d",&t);
    while(t--)
    {
        string a;
        cin>>a;
        int flag=1;
        int len=a.size();
        for(int i=2;i<len;i++)
        {
            if(a[i]=='?'&&a[i-1]=='0'&&(a[i-2]=='+'||a[i-2]=='*'))
                a[i]='+';
        }
        for(int i=0;i<len&&flag;i++)
        {
            if(a[i]=='?') {a[i]='1';continue;}
            if(a[i]=='+'||a[i]=='*')
            {
                if(i==len-1||i==0) flag=0;
                else if(a[i+1]=='+'||a[i+1]=='*') flag=0;
            }
            else if(a[i]=='0')
            {
                if(i==0&&len>1&&(a[i+1]!='+'&&a[i+1]!='*'&&a[i+1]!='?')) {flag=0;continue;} 
                if((i-1)<0||a[i-1]=='+'||a[i-1]=='*') 
                    if(i+1<len)
                    {
                        if(a[i+1]=='?') a[i+1]='+'; 
                        else if(a[i+1]!='+'&&a[i+1]!='*') flag=0;
                    }
            }
        }
        if(!flag)
            printf("IMPOSSIBLE\n");
        else
            cout<<a<<endl;
    }
    return 0;
}

L.  Graph Theory Homework 水，得到结论：根号函数的性质：$\sqrt{a+b+c+…}\le\sqrt{a}+\sqrt{b}+\sqrt{c}+…$

展开全文 >>

Journey with Knapsack(令人自闭的母函数+五边形定理)

 Journey with Knapsack

题意

有一个容量为2n的背包，n种食物，每种食物的体积为i，最多有$a_i$个，除了食物，还有m件装备，每件装备的体积是$b_i$，必须带一件装备，问2n的背包能够装下的所有情况种数？

1<=n<=5e4 , 0<=ai<=2n , 1<=m<=2n，0<=bi<=2n。

思路

背包全部装食物的方案数：

$$
\prod_{i=1}^n(1+x^i+x^{2i}+…+x^{a_ii})=\prod_{i=1}^n\frac{1-x^{i(a_i+1)}}{1-x^i}
$$

$$
=\prod_{i=1}^n(1-x^{i(a_i+1)}) \prod_{i=1}^n(\frac{1}{1-x^i})
$$

对于左边的累乘进行分析：

  1. 假设右边部分已经求得，是一个2n项（后面会求到）多项式：$\sum_{i=1}^{2n}dp[i]*x^i$(dp[i]的i指的是体积，dp的值是种数)
  2. 那么原式子就变成，左边的n个两项式与右边的的2n项式相乘，有：

$$
(1-x^{i(a_i+1)})(\sum_{j=1}^{2n}dp[j]x^j)
$$

$$
=\sum_{j=1}^{2n}dp[j]x^j-\sum_{j=1}^{2n}dp[j]x^{i(a_i+1)+j}
$$

​ 我们将j向右移$i*(a_i+1)$位，则：

$$
=\sum_{j=1}^{2n}dp[j]x^j-\sum_{j=i(a_i+1)}^{2n+i(a_i+1)}dp[j-i(a_i+1)]x^j
$$

$$
=\sum_{j=1}^{i(a_i+1)}dp[j]x^j+\sum_{j=i(a_i+1)}^{2n}(dp[j]-dp[j-i(a_i+1)])x^j
$$

 （由于2n以后的项都没有意义，所以可以减少到2n）
  1. 由于前面的假设1，dp[j]已经求得，因此我们只要再求得对所有$i*(a_i+1)\le{j}\le2n$，再求：

$$
dp[j]=dp[j]-dp[j-i*(a_i+1)]
$$

对于右边的累乘：
$$
\prod_{i=1}^n(\frac{1}{1-x^i}) = \prod_{i=1}^{2n}(\frac{1}{1-x^i}) \prod_{i=n+1}^{2n}({1-x^i})（不满2n所以补上）
$$

  1. 对于左边的式子，根据五边形定理：

$$
Q(x)=\sum_{i\ge1}(1-x^i)=\sum_{i\ge1}(-1)^i(x^{\frac{3i^2-i}{2}}+x^{\frac{3i^2+i}{2}})=(1-x)(1-x^2)…=1-x-x^2+x^5+x^7+……
$$

​ 整数拆分的式子是这样的：
$$
P(x)=(1+x+x^2+…)（1+x^2+x^4+…）(1+x^3+x^6+…)
$$

$$
=\prod_{i\ge1}(1+x^i+x^{2i}+…)=\prod_{i\ge1}\frac{1}{1-x^i} （x<1无穷等比数列求级数）
$$

​ 因此我们可以看到：Q(x)P(x)=1，也就是说：
$$
(1-x-x^2+x^5+x^7+……)(1+p(1)x+p(2)x^2+p(3)x^3+…)=1
$$
​ 因此我们考虑，对于每项x^n前面的系数，必定有：
$$
p(n)-p(n-1)-p(n-1)+p(n-5)+p(n-7)……=0
$$
​ 因此得递推式：
$$
p(n)=p(n-1)+p(n-1)-p(n-5)-p(n-7)……
$$
​ 可以求出dp[i]=p[i]。（i<=2n）

  1. 对于右边的式子$\prod_{i=n+1}^{2n}({1-x^i})$，由于累乘$x^a*x^b=x^{(a+b)}$，故对于a+b>2n的都可以舍去。

    就化为了：

$$
1-\sum_{i=n+1}^{2n}x^i
$$

  1. 整个式子就变成：

$$
P(x)(1-\sum_{i=n+1}^{2n}x^i),P(x)=\sum_{i=1}^{2n}dp[i]x^i
$$

​
$$
=\sum_{i=1}^{2n}dp[i]x^i -\sum_{i=n+1}^{2n}dp[i-n-1]x^i-\sum_{i=n+2}^{2n}dp[i-n-2]x^i-……
$$

$$
=\sum_{i=1}^{n}dp[i]x^i+x^{n+1}(dp[n+1]-dp[0])+x^{n+2}(dp[n+2]-dp[1]-dp[0])+……
$$

$$
+x^{2n}(dp[2n]-dp[n-1]-dp[n-2]-…-dp[0])
$$

​ 也就是说对于所有dp[i]，i>=n+1,<=2n的，都进行减去sum[i-n-1] (前缀和)的操作。即：
$$
dp[i]=dp[i]-\sum_{j=1}^{i-n-1}dp[j]
$$
​ 那么所有的部分就都算完啦！！！！！！

啊啊啊啊啊啊啊啊啊啊啊啊啊

看！代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
#include <bits/stdc++.h>
using namespace std;
typedef long long LL;
const LL INF = 1e9+5;
const int MAXN = 100005;
const LL MOD = 1e9+7;
using namespace std;
int n;
long long q[2005],f[MAXN];
long long dp[MAXN];
void five()
{
    for(int i=1;i<=2000;i+=2)
    {
        LL temp=(i+1)/2;
        q[i]=(3*temp*temp-temp)/2;
        q[i+1]=(3*temp*temp+temp)/2;
    }
    f[0]=1;
    for(int i=1;i<=MAXN;i++)
    {
        for(int j=1,c=1;j<=2000;j+=2,c*=-1)
        {
            if(i-q[j]<0) break;
            f[i]=(f[i]+f[i-q[j]]*c+MOD)%MOD;
            if(i-q[j+1]<0) break;
            f[i]=(f[i]+f[i-q[j+1]]*c+MOD)%MOD;
        }
    }
}
int main()
{
    int n,m,cas=1;
    LL a;
    five();
    while(~scanf("%d%d",&n,&m))
    {
        for(int i=0;i<=(n<<1);i++) dp[i]=f[i];
        for(int i=1;i<=n;i++)
        {
            scanf("%lld",&a);
            LL b=(a+1)*i;
            for(int j=n<<1;j>=b;j--) 
                dp[j]=(dp[j]-dp[j-b]+MOD)%MOD;
        }
        for(int i=n+1,sum=0;i<=(n<<1);i++)
        {
            sum=(sum+dp[i-n-1])%MOD;
            dp[i]=(dp[i]-sum+MOD)%MOD;
        }
        long long ans=0;
        while(m--)
        {
            scanf("%lld",&a);
            ans=(ans+dp[2*n-a])%MOD;
        }
        printf("Case #%d: %lld\n",cas++,ans);
    }
    return 0;
}
/** 来自大神的参考思想！！
HDU 6042 - Journey with Knapsack [ 生成函数,五边形定理 ]  |  2017 Multi-University Training Contest 1
题意:
    n种物品，每种 a[i] 个，体积为 i，m 个武器，每个体积为 b[i]
    求2*n大小的背包里只能装一个武器，任意食物的方案数
    限制条件：
        a[i]各不相同且 0 <= a[1] <= a[2] <= ... a[n] <= 2*n
        n <= 5e4
分析：
    先不考虑武器，求出任意i <= 2*n 的放食物的方案数ans[2*n]，答案即为 ∑ ans[2*n - b[i]]
    其实本质和整数划分相同，限制了每个数字选择的次数
    考虑选择食物的生成函数：
        第i种食物的贡献因子 f(x) = 1 + x^i + x^2i + ... + x^(a[i]*i) = ( 1 - x^((ai+1)*i) ) / ( 1 - x^i )
    故   F(x) =  ∏ f(i) [1<=i<=n]
             = ∏ (1 - x^((ai+1)*i)) / (1-x^i) [1<=i<=n]
             = ∏ (1 - x^((ai+1)*i)) [1<=i<=n]  *  ∏ 1/(1-x^i) [1<=i<=n]
 ///////////////////////////////////////////////////////////
    研究一下乘号左边这一项累乘：
        假设已求得乘号右边这一项 F'(x) = ∏ 1/(1-x^i) [1<=i<=2*n] = ∑ dp[i]*x^i [1<=i<=2*n]
        则两边多项式合并时，相当于一个n项的多项式（右边） 和 n个两项的多项式（左边）相乘
        假设左边第i项 (1 - x^((ai+1)*i)) 与 F'(x) 合并，则：
            (1 - x^((ai+1)*i)) * ( ∑ dp[j]*x^j [1<=j<=2*n] ) =
             ∑ dp[j]*x^j [1<=j<=n] - ∑ dp[j-(ai+1)*i] * x^j [(ai+1)*i) <= j <= 2*n+(ai+1)*i)]
              （多项式右移(ai+1)*i)次）
        由于体积只有2*n大小，故x^(2*n+1)项及以后无意义
            故上式 = ∑ dp[j]*x^j [1<=j<=n]  -  ∑ dp[j-(ai+1)*i] * x^j [(ai+1)*i) <= j <= 2*n]
                   = ∑ dp[j]*x^j [1<=j< (ai+1)*i)]  +  ∑ (dp[j]- dp[j-(ai+1)*i])*x^j [(ai+1)*i) <= j <= 2*n]
        即对于所有 (ai+1)*i <= j <= 2*n 的项，执行操作：
            dp[j] = dp[j] - dp[j-a(i+1)*i] （按01背包形式，至高往低）

        由于合并后 F'(x) 形式不变，故可循环合并 n 次
        单次合并复杂度 O(2*n - a(i+1)*i) = O(n)
        根据限制条件 0 <= a[1] <= a[2] <= ... a[n] <= 2*n ，可推得 ai >= i-1, (ai+1)*i >= i^2 （鸽巢原理）
        故 (ai+1)*i <= 2*n 的项只有 O(n^0.5) 项
        故合并总时间复杂度 O(n^1.5)
 //////////////////////////////////////////
    研究一下乘号右边这一项累乘：
        其形式与无限制的整数划分的方案数的生成函数相同，由于目前只有n项累乘，按题意先补齐至2n项
        F'(x) = ∏ 1/(1-x^i) [1<=i<=n]
              = ∏ 1/(1-x^i) [1<=i<=2n]  *  ∏ (1-x^i) [n+1<=i<=2n]

        乘号左边这一项 P(x) 即2*n以内无限制的整数划分的方案数，根据五边形定理可以在 O(n^1.5) 预处理出

        观察乘号右边那一项，虽然形式与上面讨论的累乘形式相近，但可以分析暴力合并复杂度 O(n^2)
        打开这个累乘，由于 n+1<=i<=2n ，任意两项 x^i * x^j = x^(i+j) ，此时i+j > 2*n
        故去掉指数为 2n 以上的无效项后：
        ∏ (1-x^i) [n+1<=i<=2n]  =  1 - ∑x^i [n+1<=i<=2n]
        F'(x) = P(x)  *  ( 1 - ∑x^i ) [n+1<=i<=2n]
        令   P(x) = ∑ dp[i]*x^i [1<=i<=2n]，考虑合并：
        F'(x) =   ∑ dp[i] * x^i [1<=i<=2n]
                - ∑ dp[i-n-1] * x^i [n+1<=i<=2n]
                - ∑ dp[i-n-2] * x^i [n+2<=i<=2n]
                - ∑ dp[i-n-3] * x^i [n+3<=i<=2n]
                - ...
              =   ∑ dp[i] * x^i [1<=i<=n]
                + ∑ x^(n+1)  *  (dp[n+1] - dp[0])
                + ∑ x^(n+2)  *  (dp[n+1] - dp[0] - dp[1])
                + ∑ x^(n+2)  *  (dp[n+1] - dp[0] - dp[1] - dp[2])
                ...
        即对于所有 n+1 <= j <= 2*n 的项，执行操作：
            dp[j] = dp[j] - sum[j-n-1],  sum[]为dp[]的前缀和
        合并复杂度O(n)

    总时间复杂度O(n^1.5)
*/

展开全文 >>

tag:

    缺失模块。
    1、请确保node版本大于6.2
    2、在博客根目录（注意不是yilia根目录）执行以下命令：
    npm i hexo-generator-json-content --save

    3、在根目录_config.yml里添加配置： 

      jsonContent:
    meta: false
    pages: false
    posts:
      title: true
      date: true
      path: true
      text: false
      raw: false
      content: false
      slug: false
      updated: false
      comments: false
      link: false
      permalink: false
      excerpt: false
      categories: false
      tags: true

小可爱的小可爱，<br/>拖肥的娘亲，<br/>划水的ACMer，<br/>努力中的小菜鸡，<br/>想要自信和一往无前的勇气。